题目内容
10.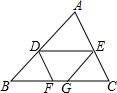 如图,在△ABC中,DE∥BC,DF∥AC,EG∥AB,且AE:EC=3:2,若BC=10,则FG的长为( )
如图,在△ABC中,DE∥BC,DF∥AC,EG∥AB,且AE:EC=3:2,若BC=10,则FG的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据平行线分线段成比例,由DE∥BC得到$\frac{DE}{BC}$=$\frac{AE}{AC}$,则$\frac{DE}{10}$=$\frac{3}{5}$,解得DE=6,再证明四边形DECF为平行四边形得到FC=DE=10,接着由EG∥AB得到$\frac{CG}{10}$=$\frac{2}{5}$,解得CG=4,然后计算FC-CG即可.
解答 解:∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$,
∵AE:EC=3:2,BC=10,
∴$\frac{DE}{10}$=$\frac{3}{5}$,
解得DE=6,
∵DE∥FC,DF∥AC,
∴四边形DECF为平行四边形,
∴FC=DE=10,
∵EG∥AB,
∴$\frac{CG}{CB}$=$\frac{CE}{CA}$,即$\frac{CG}{10}$=$\frac{2}{5}$,解得CG=4,
∴FG=FC-CG=6-4=2.
故选B.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了平行四边形的判定与性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
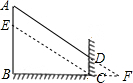 如图,一位同学想利用影子测量旗杆的高度,在同一时刻,测得一米长的标杆的影长为1.2米,但他测旗杆影子时,因旗杆靠近教室,影子的一部分落在了墙上.他先测得地面部分的影子长为12米,又测得墙上影高为2米,求旗杆的高度AB.
如图,一位同学想利用影子测量旗杆的高度,在同一时刻,测得一米长的标杆的影长为1.2米,但他测旗杆影子时,因旗杆靠近教室,影子的一部分落在了墙上.他先测得地面部分的影子长为12米,又测得墙上影高为2米,求旗杆的高度AB.