题目内容
1.在平行四边形ABCD中,AB=2BC,M是AB的中点,求证:DM⊥CM.分析 首先根据题意画出图形,由在平行四边形ABCD中,AB=2BC,M是AB的中点,易得AD=AM=BM=BC,继而证得DM,CM分别是∠ADC与∠BCD的角平分线,继而证得结论.
解答 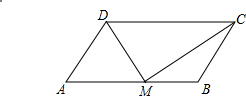 证明:如图,∵四边形ABCD是平行四边形,
证明:如图,∵四边形ABCD是平行四边形,
∴AB=BC,
∵AB=2BC,M是AB的中点,
∴AD=BC=AM=BM,
∴∠ADM=∠AMD,∠BCM=∠BMC,
∵AB∥CD,
∴∠CDM=∠AMD,∠DCM=∠BMC,
∴∠ADM=∠CDM,∠BCM=∠DCM,
∵AD∥BC,
∴∠ADC=∠BCD=180°,
∴∠CDM+∠DCM=$\frac{1}{2}$∠ADC+$\frac{1}{2}$∠BCD=90°,
∴∠CMD=90°,
即CM⊥DM.
点评 此题考查了平行四边形的性质、等腰三角形的判定与性质以及角平分线的性质.注意根据题意作出图形,结合图形求解是关键.

练习册系列答案
相关题目
9.用围棋子按下面的规律摆图形,则摆第2012个图形需要围棋子的枚数是( )


| A. | 6035 | B. | 6038 | C. | 6041 | D. | 6044 |
16.平行四边形不一定具有的特征是( )
| A. | 两组对边分别平行 | B. | 两组对角分别相等 | ||
| C. | 对角线相等 | D. | 内角和为360° |
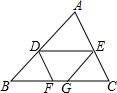 如图,在△ABC中,DE∥BC,DF∥AC,EG∥AB,且AE:EC=3:2,若BC=10,则FG的长为( )
如图,在△ABC中,DE∥BC,DF∥AC,EG∥AB,且AE:EC=3:2,若BC=10,则FG的长为( )