题目内容
已知点A在直线y=-2x+4上，若过点A和原点的直线及该直线和x轴所围成的三角形的面积为2，则点A的坐标为（ ）
| A、（1，2） |
| B、（3，-2） |
| C、（1.5，1） |
| D、（1，2）或（3，-2） |
考点：一次函数图象上点的坐标特征
专题：计算题,数形结合
分析：设A（a，-2a+4）．根据函数解析式求得点B的坐标，则易求OB的长度．然后由三角形的面积公式来求a的值．
解答：
解：如图，设直线y=-2x+4与x轴交于点B．设A（a，-2a+4）．
令y=0，则-2x+4=0，
解得，x=2，
所以B（2，0），则OB=2．
所以
OB•|-2a+4|=
×2|-2a+4|=2，即-2a+4=±2，
解得，a=1或a=3，
所以A（1，2）或（3，-2）．
故选：D．
解：如图，设直线y=-2x+4与x轴交于点B．设A（a，-2a+4）．令y=0，则-2x+4=0，
解得，x=2，
所以B（2，0），则OB=2．
所以
| 1 |
| 2 |
| 1 |
| 2 |
解得，a=1或a=3，
所以A（1，2）或（3，-2）．
故选：D．
点评：本题考查了一次函数图象上点的坐标特征．解题时注意a有2个值．
练习册系列答案
相关题目
如图，函数y1=| k1 |
| x |
| A、x＞1 |
| B、-1＜x＜0 |
| C、-1＜x＜0或x＞1 |
| D、x＜-1或0＜x＜1 |
下列语句表示命题的是（ ）
| A、作∠A的平分线 |
| B、直角都相等吗？ |
| C、画一条直线 |
| D、内错角不相等 |
在同一直角坐标平面内，如果直线y=k1x与双曲线y=
没有交点，那么k1和k2的关系一定是（ ）
| k2 |
| x |
| A、k1+k2=0 |
| B、k1•k2＜0 |
| C、k1•k2＞0 |
| D、k1=k2 |
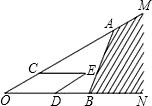如图，点A、B分别在射线OM、ON上，C、D分别是线段OA和OB上的点，以OC、OD为邻边作平行四边形OCED，下面给出三种作法的条件：①取OC=
如图是由几块小立方块所搭成的几何体从上面看到的图，小正方体中的数字表示该位置小立方块的个数，请画出从正面看到的图与从左面看到的图．