题目内容
6. 某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%
某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%(盈利率=$\frac{售价-进价}{进价}$×100%).
(1)求这种衣服每件进价是多少元?
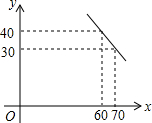
(2)商店决定试销售这种衣服时,每件售价不低于进价,又不高于70元,若试销售中销售量y(件)与每件售价x(元)的关系是一次函数(如图).求出y与x的函数关系式,并写出x的范围;
(3)当每件售价为多少元时,商店销售这种衣服的利润最大?
分析 (1)根据等量关系盈利率=$\frac{售价-进价}{进价}$×100%,设出进价为a元,列方程解答即可;
(2)利用图象求出销售量y(件)与每件售价x(元)的关系是一次函数,进一步根据利润=每件利润×销售量,求得y与x的函数关系式,
(3)列出二次函数根据x的取值范围求得最大值和售价即可.
解答 解:(1)设购进这种衣服每件需a元,依题意得:
60-a=20%a,
解得:a=50,
答:购进这种衣服每件需50元;
(2)设一次函数解析式为y=kx+b,由图象可得:
$\left\{\begin{array}{l}60k+b=40\\ 70k+b=30\end{array}$,解得:k=-1,b=100,
∴y=-x+100.(50≤x≤70),
(3)设利润为w元
∴利润为:w=(x-50)(-x+100)
=-x2+150x-1500,
∵函数w=-(x-75)2+625的图象开口向下,对称轴为直线x=75,
∴当50≤x≤70时,w随x的增大而增大,
∴当x=70时,w最大=600.
答:当销售单价定为70元时,商店销售这种衣服的利润最大.
点评 此题考查二次函数的实际应用,注意求出每件利润及销售量,根据销售问题中的基本等量关系:利润=每件利润×销售量,列函数式.

练习册系列答案
相关题目
17.在式子:-$\frac{3}{5}$ab,$\frac{2{x}^{2}y}{5}$,$\frac{x+y}{2}$,-a2bc,1,x2-2x+3中,单项式个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
15.下列说法正确的是( )
| A. | 0.720精确到0.001 | B. | 3.6万精确到个位 | ||
| C. | 5.078精确到百分位 | D. | 数字3000是一个近似数 |
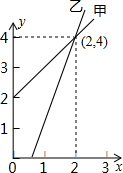 如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论:
如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论: 结合图形计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$=$\frac{127}{128}$.
结合图形计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$=$\frac{127}{128}$.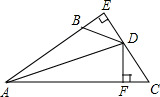 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.