题目内容
14.在有理式$\frac{x}{2}+y,\frac{3}{-x},\frac{a}{3},\frac{1}{5}(x+y),\frac{xy}{x}$中,是分式的有2个.分析 判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
解答 解:$\frac{3}{-x}$,$\frac{xy}{x}$是分式,
故答案为:2;
点评 本题主要考查分式的定义,分母中含有字母则是分式,如果不含有字母则不是分式.

练习册系列答案
相关题目
5.若y=$\frac{k}{x}$的图象在第二、四象限,则y=kx+1的图象所在象限是( )
| A. | 一、二、三 | B. | 二、三、四 | C. | 一、三、四 | D. | 一、二、四 |
3.下列各式中,正确的是( )
| A. | 2a+3b=5ab | B. | 7ab-3ab=4 | C. | x2y-2x2y=-x2y | D. | a3+a2=a5 |
4.观察下列代数式:2x2,-3,a+b,πr2,-$\frac{3}{x}$,其中单项式有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
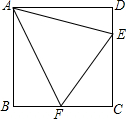 正方形ABCD中,∠EAF=45°.求证:EF=BF+DE.
正方形ABCD中,∠EAF=45°.求证:EF=BF+DE. 某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%
某商店决定购进一批某种衣服.若商店以每件60元卖出,盈利率为20%