题目内容
11.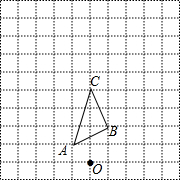 如图,正方形网格中的每一个小正方形的边长为1个单位长度,题中所给各点均在格点上.
如图,正方形网格中的每一个小正方形的边长为1个单位长度,题中所给各点均在格点上.(1)以图中的点O为位似中心,将△ABC作位似变换且放大到原来的2倍,得到△A1B1C1,画出△A1B1C1;
(2)连接CO、AO,完成下面填空:
①$\frac{{S}_{△{A}_{1}{B}_{1}{C}_{1}}}{{S}_{△ABC}}$=4,tan∠ACO=$\frac{1}{3}$;sin∠BCO=$\frac{\sqrt{5}}{5}$.
分析 (1)画位似图形的一般步骤为:①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据位似比,确定能代表所作的位似图形的关键点;④顺次连接上述各点,得到放大或缩小的图形;
(2)相似三角形的面积的比等于相似比的平方,据此计算即可.
解答 解:(1)如图所示,△A1B1C1即为所求;
(2)∵△A1B1C1∽△ABC,且相似比为2,
∴$\frac{{S}_{△{A}_{1}{B}_{1}{C}_{1}}}{{S}_{△ABC}}$=22=4,
由图可得,tan∠ACO=$\frac{1}{3}$,sin∠BCO=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
故答案为:4,$\frac{1}{3}$,$\frac{\sqrt{5}}{5}$.
点评 本题主要考查了利用位似进行作图以及相似三角形的性质的运用,解题时注意:画一个图形的位似图形时,位似中心的选择是任意的,这个点可以在图形的内部或外部或在图形上,对于具体问题要考虑画图方便且符合要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.若直线y=kx+b经过A(0,2)和B(3,0)两点,那么这个一次函数关系式是( )
| A. | y=2x+3 | B. | y=3x+2 | C. | y=-$\frac{2}{3}$x+2 | D. | y=x-1 |
16.绝对值小于π的整数的和( )
| A. | 3 | B. | 4 | C. | 0 | D. | 7 |
20.已知整数a1,a2,a3,a4…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…,依此类推,则a2016的值为( )
| A. | -1007 | B. | -1008 | C. | -1009 | D. | -2016 |

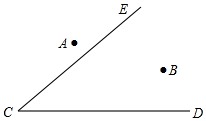 如图,在∠DCE内部找一个点P,使点P到A、B两点的距离相等且到∠DCE两边的距离也相等,请作出点P(尺规作图,不要求写作法,保留作图痕迹).
如图,在∠DCE内部找一个点P,使点P到A、B两点的距离相等且到∠DCE两边的距离也相等,请作出点P(尺规作图,不要求写作法,保留作图痕迹).