题目内容
1.在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“非常距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1与点P2的“非常距离”为|x1-x2|;
若|x1-x2|<|y1-y2|,则点P1与点P2的“非常距离”为|y1-y2|.
例如:点P1(1,2),点P2(3,5),因为|1-3|<|2-5|,所以点P1与点P2的“非常距离”为|2-5|=3,也就是图1中线段P1Q与线段P2Q长度的较大值(点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点).

(1)已知点A(0,1),B为y轴上的一个动点,
①若点A与点B的“非常距离”为3,写出一个满足条件的点B的坐标;
②直接写出点A与点B的“非常距离”的最小值;
(2)已知M是直线y=-$\frac{1}{2}$x-2上的一个动点,
①如图2,点N的坐标是(-2,0),求点M与点N的“非常距离”d的最小值及相应的点M的坐标;
②若P是坐标平面内的一个动点,且OP=$\frac{\sqrt{5}}{2}$,直接写出点M与点P的“非常距离”d的最小值及相应的点P和点M的坐标.
分析 (1)①根据点B位于y轴上,可以设点B的坐标为(0,y).由“非常距离”的定义可以确定|1-y|=3,据此可以求得y的值;
②设点B的坐标为(0,y),根据|0-0|≥|1-y|,得出点A与点B的“非常距离”最小值为|0-0|=0,即可得出答案;
(2)①先确定出M点的位置,由M在直线y=-$\frac{1}{2}$x-2上,设出M点坐标,由条件可求得M点坐标及点M与点N的“非常距离”d的最小值;
②当点P在过原点且与直线y=-$\frac{1}{2}$x-2垂直的直线上时,点M与点P的“非常距离”最小,求出P(-$\frac{1}{2}$,-1),进而求解即可.
解答 解:(1)①∵B为y轴上的一个动点,
∴设点B的坐标为(0,y).
∵|0-0|=0≠3,
∴|1-y|=3,
解得,y=4或y=-2;
∴点B的坐标是(0,4)或(0,-2);
②点A与点B的“非常距离”的最小值为0;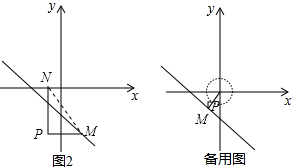 (2)①过N点作x轴的垂线,过M点作y轴的垂线,两条垂线交于点P,
(2)①过N点作x轴的垂线,过M点作y轴的垂线,两条垂线交于点P,
连结MN,当点M在点N的右下方且使△PMN为等腰直角三角形时,点M与点N的“非常距离”最小.
设点M的坐标为(x0,-$\frac{1}{2}$x0-2),由PM=PN得|x0+2|=|$\frac{1}{2}$x0+2|,解得:x0=0,或x0=-$\frac{8}{3}$,
∴点M的坐标为(0,-2)或(-$\frac{8}{3}$,-$\frac{2}{3}$),∴PM=PN=2,或$\frac{2}{3}$,
∴点M与点N的“非常距离”的最小值为$\frac{2}{3}$,相应的M的坐标为(-$\frac{8}{3}$,-$\frac{2}{3}$);
②当点P在过原点且与直线y=-$\frac{1}{2}$x-2垂直的直线上时,点M与点P的“非常距离”最小,设P(x,y)(点P位于第三象限).
则$\left\{\begin{array}{l}{\frac{y}{x}=2}\\{{x}^{2}+{y}^{2}=\frac{5}{4}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=-1}\end{array}\right.$,
故P(-$\frac{1}{2}$,-1).
-$\frac{1}{2}$-x0=-1+$\frac{1}{2}$x0+2,
解得x0=-1,
则点M的坐标为(-1,-$\frac{3}{2}$),最小值为$\frac{1}{2}$.
点评 本题考查了一次函数综合题.对于信息给予题,一定要弄清楚题干中的已知条件.理解题中“非常距离”的定义是正确解题的关键.

 已知:如图,四边形ABCD是平行四边形,在边AB的延长线上截取BE=AB,点F在AE的延长线上,CE和DF交于点M,BC和DF交于点N.联结BD.
已知:如图,四边形ABCD是平行四边形,在边AB的延长线上截取BE=AB,点F在AE的延长线上,CE和DF交于点M,BC和DF交于点N.联结BD.