题目内容
阅读下面材料:
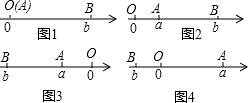
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.
当A、B两点中有一点在原点时,不妨设点A在原点,
如图1,|AB|=|OB|=|b|=|a-b|;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
如图3,点A、B都在原点的左边,
|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
如图4,点A、B在原点的两边,
|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|;
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上表示x和3的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
(3)当式子|x+1|+|x-3|取最小值时,相应的x的取值范围是 .
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.
当A、B两点中有一点在原点时,不妨设点A在原点,
如图1,|AB|=|OB|=|b|=|a-b|;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
如图3,点A、B都在原点的左边,
|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
如图4,点A、B在原点的两边,
|AB|=|OB|+|OA|=|a|+|b|=a+(-b)=|a-b|;

回答下列问题:
(1)数轴上表示2和5的两点之间的距离是
(2)数轴上表示x和3的两点A和B之间的距离是
(3)当式子|x+1|+|x-3|取最小值时,相应的x的取值范围是
考点:绝对值,数轴
专题:
分析:(1)根据数轴上两点间的距离的表示方法分别解答即可;
(2)根据两点间的距离的表示方法列式,再根据绝对值的性质求解即可;
(3)表示到-1和3的距离的和最小的值.
(2)根据两点间的距离的表示方法列式,再根据绝对值的性质求解即可;
(3)表示到-1和3的距离的和最小的值.
解答:解:(1)数轴上表示2和5的两点之间的距离是|5-2|=3,
数轴上表示-2和-5的两点之间的距离是|(-2)-(-5)|=3,
数轴上表示1和-3的两点之间的距离是|-3-1|=4;
(2)|x-3|,
AB=2,则|x-3|=2,
所以,x-3=2或x-3=-2,
解得x=5或x=1;
(3)表示到-1和3的距离的最小值,
|x+1|+|x-3|取最小值时,相应的x的取值范围是-1≤x≤3.
故答案为:(1)3,3,4;(2)|x-3|,5或1;(3)-1≤x≤3.
数轴上表示-2和-5的两点之间的距离是|(-2)-(-5)|=3,
数轴上表示1和-3的两点之间的距离是|-3-1|=4;
(2)|x-3|,
AB=2,则|x-3|=2,
所以,x-3=2或x-3=-2,
解得x=5或x=1;
(3)表示到-1和3的距离的最小值,
|x+1|+|x-3|取最小值时,相应的x的取值范围是-1≤x≤3.
故答案为:(1)3,3,4;(2)|x-3|,5或1;(3)-1≤x≤3.
点评:本题考查了绝对值和数轴,读懂题目信息,理解数轴上两点间的距离的表示方法是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
△ABC中,AB=AC,AB的垂直平分线与直线AC相交所成锐角为40°,则此等腰三角形的顶角为( )
| A、50° | B、60° |
| C、130° | D、50°或130° |
两个全等图形中可以不同的是( )
| A、位置 | B、长度 | C、角度 | D、面积 |
在①(-1)0=1,②(-1)1=-1,③3a-2=
,④(-x)5÷(-x)3=-x2中,其中正确的式子有( )
| 1 |
| 3a2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列方程中是一元二次方程的是( )
| A、2x+1=0 | ||
| B、y2+x=1 | ||
| C、x2+1=0 | ||
D、
|
 已知△ABC,AB边中点为D,E、F分别在AC、BC边上运动,求证:S△DEF≤S△ADE+S△BDF.
已知△ABC,AB边中点为D,E、F分别在AC、BC边上运动,求证:S△DEF≤S△ADE+S△BDF.