题目内容
19.在平面直角坐标系xOy中,以原点O为圆心的圆过点A(-13,0),直线y=kx+3k-4与⊙O交于B、C两点,则弦BC的长的最小值为24.分析 根据直线y=kx-3k-4必过点D(3,-4),求出最短的弦CB是过点D且与该圆直径垂直的弦,再求出OD的长,再根据以原点O为圆心的圆过点A(-13,0),求出OB的长,再利用勾股定理求出BD,即可得出答案.
解答  解:∵直线y=kx-3k-4必过点D(3,-4),
解:∵直线y=kx-3k-4必过点D(3,-4),
∴最短的弦CB是过点D且与该圆直径垂直的弦,
∵点D的坐标是(3,-4),
∴OD=5,
∵以原点O为圆心的圆过点A(-13,0),
∴圆的半径为13,
∴OB=13,
∴BD=12,
∴BC的长的最小值为24.
故答案为:24.
点评 此题考查的是垂径定理、勾股定理、圆的有关性质,解题的关键是求出BC最短时的位置.

练习册系列答案
相关题目
10.计算$\root{3}{64}$的结果是( )
| A. | 8 | B. | -4 | C. | 4 | D. | ±4 |
4.甲乙两战士各射靶10次,总成绩都是99.68环,甲的方差是0.28,乙的方差是0.21,则下列说法中,正确的是( )
| A. | 乙的成绩比甲的成绩稳定 | B. | 甲的成绩比乙的成绩稳定 | ||
| C. | 甲和乙成绩的稳定性相同 | D. | 无法确定甲乙成绩的稳定性 |
11.使等式$\frac{7}{x+2}$=$\frac{7x}{{x}^{2}+2x}$自左到右变形成立的条件是( )
| A. | x<0 | B. | x>0 | C. | x≠0 | D. | x≠0且x≠7 |
9.二元一次方程组$\left\{\begin{array}{l}x+y=6\\ x-3y=-2\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}x=5\\ y=1\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=-5\\ y=-1\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=4\\ y=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=-4\\ y=-2\end{array}\right.$ |
 如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5.
如图,在Rt△ABC中,∠ACB=90°,AC=3,AB=5.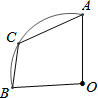 如图,在扇形OAB中,∠AOB=90°,点C在$\widehat{AB}$上,若BC=4,AC=5$\sqrt{2}$,则扇形OAB的面积为$\frac{53π}{4}$.
如图,在扇形OAB中,∠AOB=90°,点C在$\widehat{AB}$上,若BC=4,AC=5$\sqrt{2}$,则扇形OAB的面积为$\frac{53π}{4}$.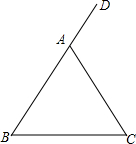 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.连结BE并延长交∠DAC的平分线AM于点F.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.连结BE并延长交∠DAC的平分线AM于点F.