Question

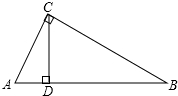
如图所示，在四边形ABCD中，AC⊥DC，△ADC的面积为30cm²，DC=12cm，AB=3cm，BC=4cm，求△ABC的面积．

Answer 1

【考点】勾股定理．

【分析】利用三角形的面积求出AC的长度，在△ABC中根据勾股定理逆定理可以得出是直角三角形．面积等于两直角边乘积的一半．

【解答】解：在Rt△ACD中，

S_△ACD=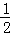AC•CD=30，

∵DC=12cm，

∴AC=5cm，

∵AB²+BC²=25，

AC²=5²=25，

∴AB²+BC²=AC²，

∴S_△ABC=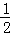AB．BC=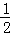×3×4=6cm²．

【点评】根据面积求出一直角边的长度，再利用勾股定理逆定理判断出直角三角形，面积就可以求出了．