Question

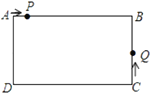
【题目】如图，在长方形中，厘米，厘米.动点从出发，以2厘米/秒的速度沿运动，到点停止运动；同时点从点出发，以4厘米/秒的速度沿运动，到点停止运动.设点运动的时间为秒（）.

（1）点在上运动时，______，______（用含的代数式表示）；点在上运动时，______，______；（用含的代数式表示）

（2）当为何值，；

（3）当为何值时，、两点在运动路线上相距的路程为4厘米；

（4）当为何值时，.

Answer 1

【答案】（1），； ，；（2）当或时，；（3）当或时，、两点相距的路程为；（4）当或时，.

【解析】

（1）根据题意直接写出答案即可；

（2）分在上运动和在上运动时，列方程求解即可；

（3）分、两点还未相遇和、两点已经相遇时，、两点在运动路线上相距的路程为4厘米，列方程求解即可；

（4）分在上运动和在上运动时，，列方程求解即可.

解：（1），，，

（2）若在上运动，

若在上运动，

∴当或时，

（3）若、两点还未相遇，则

若、两点已经相遇，则

∴当或时，、两点相距的路程为

（4）若在上运动，

若在上运动，

∴当或时，.