��Ŀ����
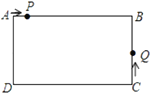
����Ŀ����֪����������A��B��Ӧ�����ֱ��ǩ�10��8��P��Q��NΪ�������������㣬��P�ӵ�A�����ٶ�Ϊÿ��2����λ����Q�ӵ�B�������ٶ�Ϊ��P��2������N��ԭ��������ٶ�Ϊÿ��1����λ��
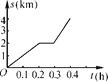
��1����P��Q���㲻��������N���߶�AB�����ȷֵ�ʱ����N����ʾ�������� ����
��2������P�����˶���ͬʱ��Q�����˶�����ʱ���P���Q���32����λ��
��3������P��Q��Nͬʱ�������˶���ʱ���N����P�͵�Q�ľ�����ȣ�
![]()
���𰸡���1��2��4����2����![]() ���P���Q���32����λ����3������0.5���N��P��Q����ľ������
���P���Q���32����λ����3������0.5���N��P��Q����ľ������
��������
��1������A��B����ʾ�����ɵ�AB��18�����ɶ���N���߶�AB�����ȷֵ�ɵô𰸣���2���辭��t���P���Q���32����λ���������P���˶�����+AB�ij�+Q���˶����룽32�����ݵ�����ϵ�г����̣��ٽ⼴�ɣ���3���辭��x���N��P��Q����ľ�����ȣ���������ɵõ�����ϵ��P��N�ľ��룽N��Q�ľ��룬���ݵ�����ϵ�г����̣��ٽ⼴�ɣ�
�⣺��1����A��B��Ӧ�����ֱ��ǩ�10��8��
��AB��18��
�߶���N���߶�AB�����ȷֵ㣬
��N���ʾ����Ϊ2��4��
�ʴ�Ϊ��2��4��
��2���辭��t���P���Q���32����λ��������ã�
2t+18+4t��32��
��ã�t��![]() ��
��
���辭![]() ���P���Q���32����λ��
���P���Q���32�����
��3���辭��x���N��P��Q����ľ�����ȣ�������ã�
10��2x+x��8��x+4x��
��ã�x��0.5��
�𣺾���0.5���N��P��Q����ľ�����ȣ�

 ���ݼ���ϵ�д�
���ݼ���ϵ�д�