Question

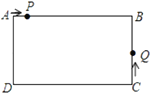
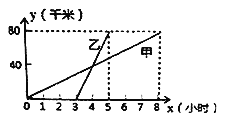
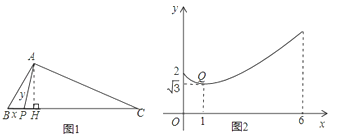
【题目】在△ABC中，AH⊥BC于点H，点P从B点开始出发向C点运动，在运动过程中，设线段AP的长为y，线段BP的长为x（如图1），而y关于x的函数图象如图2所示．Q （1，）是函数图象上的最低点．小明仔细观察图1，图2两图，作出如下结论：①AB=2；②AH=；③AC=2；④x=2时，△ABP是等腰三角形；⑤若△ABP为钝角三角形，则0＜x＜1；其中正确的是________（填写序号）．

Answer 1

【答案】①②③④

【解析】

（1）当时，的值即是的长度；

（2）图乙函数图象的最低点的值是的值；

（3）在直角中，由勾股定理来求的长度；

（3）当点运动到点时，此时，，在中，可得出，则判定是等边三角形，故，即

（5）分两种情况进行讨论，①为钝角，②为钝角，分别确定的范围即可．

解：（1）当时，的值即是的长度，故，故①正确；

（2）图乙函数图象的最低点的值是的值，故，故②正确；

（3）如图乙所示：，，则．

又，

直角中，由勾股定理得：，故③正确；

（4）在中，，，，则．

又是等腰三角形，

是等边三角形，

，即．

故④正确；

（5）①当为钝角时，此时可得；

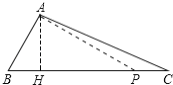
②当为钝角时，如图：过点作，则，

即当时，为钝角．

综上可得或时为钝角三角形，故⑤错误．

故答案为：①②③④．