题目内容
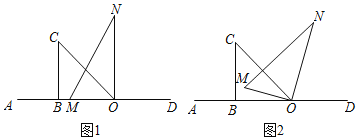
【题目】将一副直角三角板按如图1摆放在直线AD上![]() 直角三角板OBC和直角三角板MON,
直角三角板OBC和直角三角板MON,![]() ,
,![]() ,
,![]() ,
,![]() ,保持三角板OBC不动,将三角板MON绕点O以每秒
,保持三角板OBC不动,将三角板MON绕点O以每秒![]() 的速度顺时针方向旋转t秒
的速度顺时针方向旋转t秒![]()
![]() 如图2,
如图2,![]() ______度
______度![]() 用含t的式子表示
用含t的式子表示![]() ;
;
![]() 在旋转的过程中,是否存在t的值,使
在旋转的过程中,是否存在t的值,使![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
![]() 直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒
直线AD的位置不变,若在三角板MON开始顺时针旋转的同时,另一个三角板OBC也绕点O以每秒![]() 的速度顺时针旋转.
的速度顺时针旋转.
![]() 当
当![]() ______秒时,
______秒时,![]() ;
;
![]() 请直接写出在旋转过程中,
请直接写出在旋转过程中,![]() 与
与![]() 的数量关系
的数量关系![]() 关系式中不能含
关系式中不能含![]() .
.
【答案】(1)![]() (2)
(2)![]() (3)①5或10,②3∠NOD+4∠BOM=270°.
(3)①5或10,②3∠NOD+4∠BOM=270°.
【解析】
(1)把旋转前∠NOD的大小减去旋转的度数就是旋转后的∠NOD的大小.
(2)相对MO与CO的位置有两种情况,所以要分类讨论,然后根据∠NOD=4∠COM建立关于t的方程即可.
(3)①其实是一个追赶问题,分MO没有追上CO与MO超过CO两种情况,然后分别列方程即可.
②分别用t的代数式表示∠NOD和∠BOM,然后消去t即可得出它们的关系.
(1)∠NOD一开始为90°,然后每秒减少8°,因此∠NOD=90﹣8t.
故答案为:90﹣8t.
(2)当MO在∠BOC内部时,即t![]() 时,根据题意得:
时,根据题意得:
90﹣8t=4(45﹣8t)
解得:t![]() ;
;
当MO在∠BOC外部时,即t![]() 时,根据题意得:
时,根据题意得:
90﹣8t=4(8t﹣45)
解得:t![]() .
.
综上所述:t![]() 或t
或t![]() .
.
(3)①当MO在∠BOC内部时,即t![]() 时,根据题意得:
时,根据题意得:
8t﹣2t=30
解得:t=5;
当MO在∠BOC外部时,即t![]() 时,根据题意得:
时,根据题意得:
8t﹣2t=60
解得:t=10.
故答案为:5或10.
②∵∠NOD=90﹣8t,∠BOM=6t,∴3∠NOD+4∠BOM=3(90﹣8t)+4×6t=270°.
即3∠NOD+4∠BOM=270°.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数 | 1 | 2 | 3 | 4 |
线段总条数 | 3 | 6 | 10 | 15 |
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D. ![]()
【题目】某商店计划购进某型号的螺丝、螺母进行销售,有关信息如下表:
原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
螺丝 | a | 1.0 | 2.0 |
螺母 | a﹣0.3 | 0.6 | 2.0 |
(1)已知用50元购进螺丝的数量与用20元购进螺母的数量相同,求表中a的值;
(2)若该店购进螺母数量是螺丝数量的3倍还多200个,且两种配件的总量不超过3000个.
①该店计划将一半的螺丝配套(一个螺丝和两个螺母配成一套)销售,其余螺丝、螺母以零售方式销售.请问:怎样进货,才能获得最大利润?最大利润是多少?(用含a的代数式表示)
②由于原材料价格上涨,每个螺丝和螺母的进价都上涨了0.1元.按照①中的最佳进货方案,在销售价不变的情况下,全部售出后,所得利润比①少了260元,请问本次成套的销售量为多少?

【题目】小明骑自行车去学校,最初以某一速度匀速行驶,中途自行车发生故障,停下来修车耽误了几分钟,为了按时到校,他加快了速度,仍保持匀速行驶,结果准时到校,到校后,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
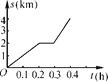
时间t/h | 0 | 0.2 | 0.3 | 0.4 |
路程s/km |
(3)路程s可以看成时间t的函数吗?