题目内容
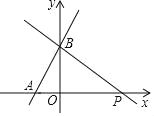
【题目】如图,在Rt△ABO中,∠OBA=90°,AB=OB,点C在边AB上,且C(6,4),点D为OB的中点,点P为边OA上的动点,当∠APC=∠DPO时,点P的坐标为 ____.

【答案】(![]() ,
,![]() )
)
【解析】
根据题意,△ABO为等腰直角三角形,由点C坐标为(6,4),可知点B为(6,0),点A为(6,6),则直线OA为![]() ,作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,交OA于点P,则点E坐标为(0,3),然后求出直线CE的解析式,联合
,作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,交OA于点P,则点E坐标为(0,3),然后求出直线CE的解析式,联合![]() ,即可求出点P的坐标.
,即可求出点P的坐标.
解:在Rt△ABO中,∠OBA=90°,AB=OB,
∴△ABO是等腰直角三角形,
∵点C在边AB上,且C(6,4),
∴点B为(6,0),
∴OB=6=AB,
∴点A坐标为:(6,6),
∴直线OA的解析式为:![]() ;
;
作点D关于OA的对称点E,点E恰好落在y轴上,连接CE,交OA于点P,

∴∠APC=∠OPE=∠DPO,OD=OE,
∵点D是OB的中点,
∴点D的坐标为(3,0),
∴点E的坐标为:(0,3);
设直线CE的解析式为:![]() ,
,
把点C、E代入,得:![]() ,
,
解得:![]() ,
,
∴直线CE的解析式为:![]() ;
;
∴ ,解得:
,解得: ,
,
∴点P的坐标为:(![]() ,
,![]() );
);
故答案为:(![]() ,
,![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目