Question

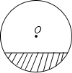
【题目】在△ABC中，AB=AC，在BC边上有两动点D、E，满足2∠DAE=∠BAC，将△AEC绕A旋转，使得AC与AB重合，点E落到点E’．

（1）求证：∠DAE’=∠DAE；

（2）当∠BE’D=20°时，求∠DEA的度数；

（3）当BD=1，EC=2，△BE’D又为直角三角形时，求∠BAC的度数．

Answer 1

【答案】（1）见解析；（2）∠DEA=80°；（3）∠BAC=90°或120°

【解析】

（1）由旋转的性质和角的和差即可得出结论；

（2）设∠DEA的度数为x．由旋转的性质得到AE’=AE，∠BAE’=∠CAE，∠AE’B=∠AEC，进而得出∠DAE’=∠DAE．用SAS证明△ADE’≌△ADE，得到∠DE’A=∠DEA=x°，进而得到∠AEC=（x+20）°．根据平角的性质得到x的值，即可得出结论；

（3）由旋转的性质及一个三角形中大边对大角得到∠BE’D不可能是直角．然后分两种情况讨论：①若∠E’BD是直角；②若∠E’DB是直角．

（1）∵将△AEC旋转得到△AE’B，

∴∠E’AB=∠EAC，

∴∠E’AD=∠EAC+∠BAD．

又∵2∠DAE=∠BAC，

∴∠DAE’=∠DAE；

（2）设∠DEA的度数为x．

∵△AEC旋转得到△AE’B，

∴AE’=AE，∠BAE’=∠CAE，∠AE’B=∠AEC．

∵2∠DAE=∠BAC，

∴∠DAE’=∠DAE．

又∵AD=AD，

∴△ADE’≌△ADE，

∴∠DE’A=∠DEA=x°．

又∵∠AE’B=∠AEC，∠BE’D=20°，

∴∠AEC=（x+20）°．

又∵∠AEC+∠AED=180°，

∴x+（x+20）=180，

∴x=∠DEA=∠DE’A=80°；

（3）∵△AEC旋转得到△AE’B，

∴BE’=EC．

又∵BD=1，BE’=2，

∴∠BE’D不可能是直角．

①若∠E’BD是直角．

∵AB=AC，

∴∠ABC=∠C．

∵△AEC旋转得到△AE’B，

∴∠ABE’=∠C．

∵∠E’BD是直角，

∴∠ABC=∠ABE’=45°，

∴∠BAC=90°．

②当∠E’DB是直角时，设AB与DE’相交于P，过P作PF垂直BE’于F．

∵∠ABC=∠ABE’，

∴PD=PF．

在Rt△BDP和Rt△BFP中，

∵BP=BP，PD=PF，

∴Rt△BDP≌Rt△BFP，

∴BD=BF．

又∵BD=1，BE’=2，

∴BF=FE’=1．

又∵PF垂直BE’于F，

∴PE’=BP，

∴∠PE’B=∠PBF．

又∵∠ABC=∠ABE’，∠E’DB是直角，

∴∠ABC=∠E’BA=∠PE’B=30°，

∴∠BAC=120°．

综上所述：∠BAC=90°或120°．