题目内容
【题目】如图,一次函数y=(m+1)x+![]() 的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为
的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为![]() .
.
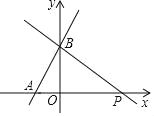
(1)求m的值及点A的坐标;
(2)过点B作直线BP与x轴的正半轴相交于点P,且OP=3OA,求直线BP的解析式.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)先求得![]()
![]() ,然后根据三角形面积求得
,然后根据三角形面积求得![]() 的长,即可求得A的坐标,把它代入y=(m+1)x+
的长,即可求得A的坐标,把它代入y=(m+1)x+![]() ,即可求得m的值;
,即可求得m的值;
(2)根据OP=3OA,可求出P的坐标,然后用待定系数法求得直线BP的解析式.
(1)由一次函数y=(m+1)x+![]() 可知:点B(0,
可知:点B(0,![]() )
)
![]() OB=
OB=![]()
![]() △OAB的面积为
△OAB的面积为![]()
![]()
![]()
![]()
把![]() 代入y=(m+1)x+
代入y=(m+1)x+![]() ,即(m+1)(-1)+
,即(m+1)(-1)+![]() =0,
=0,
解得:m=![]()
故答案是:![]() ,
,![]()
(2)![]() ,
,
![]() OP=3OA=3,
OP=3OA=3,
![]() P的坐标是
P的坐标是![]() ,
,
设直线BP的解析式为![]()
把点B(0,![]() )、点P(3,0)代入
)、点P(3,0)代入![]() 得
得

解得:![]() ,b=
,b=![]()
![]() 直线BP的解析式为
直线BP的解析式为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目