题目内容
下列句子中,是真命题的有 (填写编号)
①作一个角等于已知角
②三角形三条高线必交于三角形内一点
③三角形一条边的两个顶点到这条边上的中线所在直线的距离相等
④在△ABC中,若AB=AC=x,BC=6,则腰长x的取值范围是3<x<6
⑤在△ABC中,若AD为BC边上的中线,则AD<
(AB+AC)
①作一个角等于已知角
②三角形三条高线必交于三角形内一点
③三角形一条边的两个顶点到这条边上的中线所在直线的距离相等
④在△ABC中,若AB=AC=x,BC=6,则腰长x的取值范围是3<x<6
⑤在△ABC中,若AD为BC边上的中线,则AD<
| 1 |
| 2 |
考点:命题与定理
专题:
分析:分别利用命题的定义以及三角形三边关系以及中线的性质分别得出答案.
解答:解:①作一个角等于已知角,不是命题,故此选项错误;
②三角形三条高线必交于三角形内一点,是真命题;
③三角形一条边的两个顶点到这条边上的中线所在直线的距离相等,是真命题;
④在△ABC中,若AB=AC=x,BC=6,则腰长x的取值范围是3<x<6,是真命题;
⑤在△ABC中,若AD为BC边上的中线,则AD<
(AB+AC),
证明:如图

延长AD至E,使AD=DE,连接BE.
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴AC=BE(全等三角形的对应边相等),
在△ABE中,由三角形的三边关系可得AE<AB+BE,即2AD<AB+AC,
∴AD<
(AB+AC).
故是真命题;
故答案为:②③④⑤.
②三角形三条高线必交于三角形内一点,是真命题;
③三角形一条边的两个顶点到这条边上的中线所在直线的距离相等,是真命题;
④在△ABC中,若AB=AC=x,BC=6,则腰长x的取值范围是3<x<6,是真命题;
⑤在△ABC中,若AD为BC边上的中线,则AD<
| 1 |
| 2 |
证明:如图

延长AD至E,使AD=DE,连接BE.
在△ACD和△EBD中,
|
∴△ACD≌△EBD(SAS),
∴AC=BE(全等三角形的对应边相等),
在△ABE中,由三角形的三边关系可得AE<AB+BE,即2AD<AB+AC,
∴AD<
| 1 |
| 2 |
故是真命题;
故答案为:②③④⑤.
点评:此题主要考查了命题的概念以及全等三角形的判定及性质以及三角形的三边关系问题,正确把握相关性质是解题关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
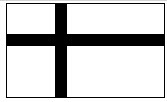 如图,要设计一幅长与宽分别为30cm,20cm的图案,其中有两条彩带,横竖彩带宽度相等,如果要使彩带所占面积是图案面积的
如图,要设计一幅长与宽分别为30cm,20cm的图案,其中有两条彩带,横竖彩带宽度相等,如果要使彩带所占面积是图案面积的 如图,已知△ABC中,点D是BA上一点,BD=AC,E,F分别是BC,DA的中点,EF和CA的延长线相交于点G.求证:AG=AF.
如图,已知△ABC中,点D是BA上一点,BD=AC,E,F分别是BC,DA的中点,EF和CA的延长线相交于点G.求证:AG=AF. 写出图中所有小于平角的角,其中O是直线AB上的一点.
写出图中所有小于平角的角,其中O是直线AB上的一点.