Question

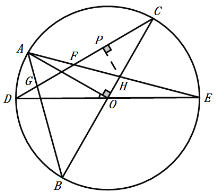
【题目】如图1，DE是⊙O的直径，点A、C是直径DE上方半圆上的两点，且AO⊥CO．连接AE，CD相交于点F，点B是直径DE下方半圆上的任意一点，连接AB交CD于点G，连接CB交AE于点H．

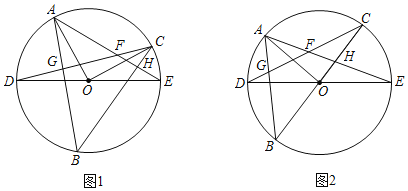
（1）∠ABC＝　 ；

（2）证明：△CFH∽△CBG；

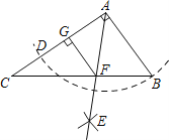
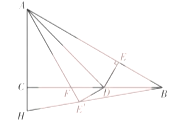
（3）若弧DB为半圆的三分之一，把∠AOC绕着点O旋转，使点C、O、B在一直线上时，如图2，求的值．

Answer 1

【答案】（1）45°；（2）见解析；（3）．

【解析】

（1），则°；

（2）如图1，，，即可求解；

（3）设，则，，则，同理可得：FC=R，由，则．

(1) ∵，

∴，

故答案为：；

(2)如图，

，，

∴，

，

∴，

，

∴；

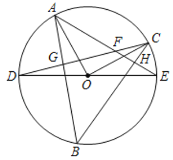
(3)如图，设∠AOD为∠1，∠COE为∠2，，圆的半径为R，

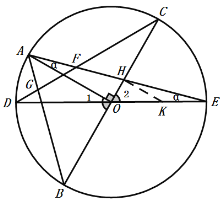
∵弧DB为半圆的三分之一，

∴，则，

∵AO⊥CO，则，

∴，

∴，

在OE上取一点K，使HK=EK，则，

设，

∵，，

∴，

在中，，，，

∴，

解得：，

，

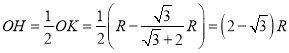则CH=CO﹣OH==(﹣1)R，

在中，，，CH=(﹣1)R，

如图，作HP⊥DC于P，

在中，，，CH=(﹣1)R，

∴，，

在中，，，

∴，

∴，

∵△CFH∽△CBG，

∴．