题目内容
17.解方程组$\left\{\begin{array}{l}{2x+y=1}\\{x-2y=3}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{2x+y=1①}\\{x-2y=3②}\end{array}\right.$,
①×2+②,得5x=5,
解得:x=1,
将x=1代入①,得y=-1,
则原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
2.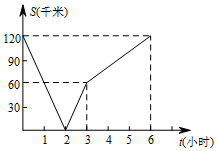 已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
 已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )
已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是( )| A. | 经过2小时两人相遇 | |
| B. | 若乙行驶的路程是甲的2倍,则t=3 | |
| C. | 当乙到达终点时,甲离终点还有60千米 | |
| D. | 若两人相距90千米,则t=0.5或t=4.5 |
6.下列方程中,解是x=1的是( )
| A. | 2x-3=1 | B. | 2x+3=1 | C. | 3x-4=-x | D. | 1.5=1-$\frac{x}{2}$ |
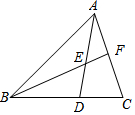 如图,在△ABC中,点D为边BC上一点,且$\frac{BD}{CD}$=$\frac{3}{2}$,点E为AD的中点,延长BE交AC于点F,则$\frac{BE}{EF}$=4.
如图,在△ABC中,点D为边BC上一点,且$\frac{BD}{CD}$=$\frac{3}{2}$,点E为AD的中点,延长BE交AC于点F,则$\frac{BE}{EF}$=4.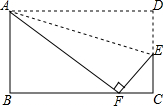 如图,小红将长方形ABCD沿AE折叠,顶点D恰好落在BC边上的F处,已知AB=8,BC=10,试求折痕AE的长.
如图,小红将长方形ABCD沿AE折叠,顶点D恰好落在BC边上的F处,已知AB=8,BC=10,试求折痕AE的长.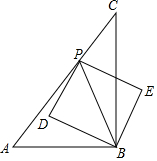 定义,若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”,如图,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA-AB以5cm/s的速度运动,当电P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
定义,若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”,如图,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA-AB以5cm/s的速度运动,当电P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).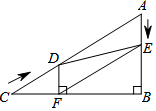 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.