题目内容
等腰三角形一腰上的高与腰长之比是1：2，则该三角形的顶角的度数是 ．
考点：含30度角的直角三角形,等腰三角形的性质
专题：
分析：分两种情况画出图形；①高在三角形的内部，②高在三角形的外部，再根据30°角所对的直角边等于斜边的一半解答即可．
解答：
解：①如图1，当高BD在三角形的内部时，
∵高BD是腰长AB的一半，
∴∠A=30°，
②如图2，当高CD在三角形的外部时，
∵高CD是腰长AC的一半，
∴∠1=30°，
∴∠BAC=180°-30°=150°，
∴该三角形的顶角的度数是30°或150°．
故答案为：30°或150°．
解：①如图1，当高BD在三角形的内部时，∵高BD是腰长AB的一半，
∴∠A=30°，
②如图2，当高CD在三角形的外部时，
∵高CD是腰长AC的一半，
∴∠1=30°，
∴∠BAC=180°-30°=150°，
∴该三角形的顶角的度数是30°或150°．
故答案为：30°或150°．
点评：本题考查了30°角所对的直角边等于斜边的一半的性质，用到的知识点是等腰三角形两腰相等的性质，注意分腰在三角形内部与外部两种情况讨论求解．
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
为了了解九年级学生的体育成绩，某校进行完体育测试后，对这次体育测试成绩进行了抽样调查，结果统计如下，其中扇形统计图中C组所在扇形的圆心角度数为36°．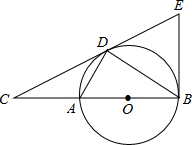
如图，点D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．
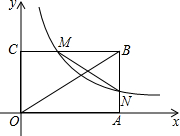如图，点A在x轴正半轴上，点C在y正半轴上，四边形OABC为矩形，面积为6，双曲线y=
如图，为了测量旗杆AB的高度，测绘员在距旗杆12m的C处，用测角仪测的旗杆顶部A的仰角为36°，已知测角仪CD的高度为1.6m，则旗杆AB的高度约为