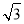题目内容
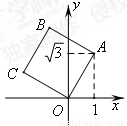
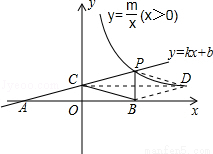
如图,一次函数y=kx+b的图象与反比例函数y= (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
(1)一次函数解析式为y=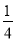 x+1,反比例解析式得:m=8,即反比例解析式为y=
x+1,反比例解析式得:m=8,即反比例解析式为y=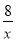 ;
;
(2)反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).
【解析】
试题分析:(1)由AC=BC,且OC垂直于AB,利用三线合一得到O为AB中点,求出OB的长,确定出B坐标,将P与B坐标代入一次函数解析式求出k与b的值,确定出一次函数解析式,将P坐标代入反比例解析式求出m的值,即可确定出反比例解析式;
(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,由一次函数解析式求出C坐标,得出直线BC斜率,求出过P且与BC平行的直线PD解析式,与反比例解析式联立求出D坐标,检验得到四边形BCPD为菱形,符合题意.
试题解析:(1)∵AC=BC,CO⊥AB,A(﹣4,0),
∴O为AB的中点,即OA=OB=4,
∴P(4,2),B(4,0),
将A(﹣4,0)与P(4,2)代入y=kx+b得: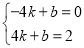 ,
,
解得:k=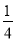 ,b=1,
,b=1,
∴一次函数解析式为y=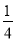 x+1,
x+1,
将P(4,2)代入反比例解析式得:m=8,即反比例解析式为y=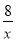 ;
;
(2)假设存在这样的D点,使四边形BCPD为菱形,如图所示,
对于一次函数y=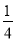 x+1,令x=0,得到y=1,即C(0,1),
x+1,令x=0,得到y=1,即C(0,1),
∴直线BC的斜率为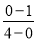 =﹣
=﹣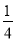 ,
,
设过点P,且与BC平行的直线解析式为y﹣2=﹣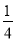 (x﹣4),即y=
(x﹣4),即y=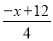 ,
,
与反比例解析式联立得: ,
,
消去y得: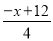 =
=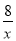 ,
,
整理得:x2﹣12x+32=0,即(x﹣4)(x﹣8)=0,
解得:x=4(舍去)或x=8,
当x=8时,y=1,
∴D(8,1),
此时PD=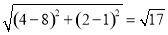 ,BC=
,BC=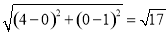 ,即PD=BC,
,即PD=BC,
∵PD∥BC,
∴四边形BCPD为平行四边形,
∵PC=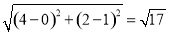 ,即PC=BC,
,即PC=BC,
∴四边形BCPD为菱形,满足题意,
则反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).
考点:反比例函数综合题.

 阅读快车系列答案
阅读快车系列答案