题目内容
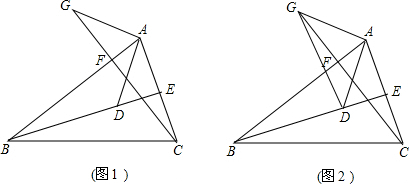
 △ABC中,BE,CF是高,相交于M,BM=AC,延长CF到N,使CN=AB,试猜想AM与AN有怎样的位置和大小关系?并证明你的结论.
△ABC中,BE,CF是高,相交于M,BM=AC,延长CF到N,使CN=AB,试猜想AM与AN有怎样的位置和大小关系?并证明你的结论.分析:由于BE,CF是高,则∠AEB=∠AFC=90°,根据等角的余角相等得到∠ABE=∠ACF,然后根据“SAS”可判断△ABM≌△NCA,则AM=AN,∠BAM=∠CNA,
由于∠CNA+∠NAF=90°,则∠NAF+∠BAM=90°,所以AM⊥AN.
由于∠CNA+∠NAF=90°,则∠NAF+∠BAM=90°,所以AM⊥AN.
解答:解:AM=AN且AM⊥AN.理由如下:
∵BE,CF是高,
∴∠AEB=∠AFC=90°,
∴∠ABE+∠BAE=∠FAC+∠ACF,
∴∠ABE=∠ACF,
在△ABM和△NCA中,
,
∴△ABM≌△NCA(SAS),
∴AM=AN,∠BAM=∠CNA,
而∠CNA+∠NAF=90°,
∴∠NAF+∠BAM=90°,
∴AM⊥AN.
∵BE,CF是高,
∴∠AEB=∠AFC=90°,
∴∠ABE+∠BAE=∠FAC+∠ACF,
∴∠ABE=∠ACF,
在△ABM和△NCA中,
|
∴△ABM≌△NCA(SAS),
∴AM=AN,∠BAM=∠CNA,
而∠CNA+∠NAF=90°,
∴∠NAF+∠BAM=90°,
∴AM⊥AN.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.

练习册系列答案
相关题目
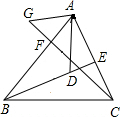 已知:如图,在△ABC中,BE、CF分别是AC、AB两条边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连AD、AG.求证:AG=AD.
已知:如图,在△ABC中,BE、CF分别是AC、AB两条边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连AD、AG.求证:AG=AD.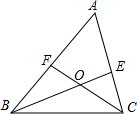 知识链接:三角形三个内角的和是180度.(如图∠A是△ABC的一个内角)如图:△ABC中,BE、CF分别是∠ABC和∠ACB的平分线,BE、CF相交于点O.
知识链接:三角形三个内角的和是180度.(如图∠A是△ABC的一个内角)如图:△ABC中,BE、CF分别是∠ABC和∠ACB的平分线,BE、CF相交于点O.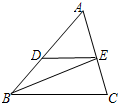 (2013•徐汇区一模)如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(2013•徐汇区一模)如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.