题目内容
 如图,△ABC中,∠ABC=90°,∠BAC=30°,△ABD、△ACE都是等边三角形,M为CE边中点,DM交AB于点N.求证:AN=NB.
如图,△ABC中,∠ABC=90°,∠BAC=30°,△ABD、△ACE都是等边三角形,M为CE边中点,DM交AB于点N.求证:AN=NB.考点:等边三角形的性质,等腰三角形的判定与性质
专题:证明题
分析:连接AM,得出AM⊥EC,∠CAM=30°,根据∠BAC=30°,得出∠BAC=∠CAM,AM=AB,再根据△ABD是等边三角形,得出AB=BD,∠ABD=60°,最后根据AM=BD,∠ABD=∠BAM,∠BND=∠ANM,证出△AMN≌△BDN,即可证出AN=NB.
解答: 解:连接AM,
解:连接AM,
∵M为CE边中点,△ACE是等边三角形,
∴AM⊥EC,
∠CAM=30°,
∵∠BAC=30°,
∴∠BAC=∠CAM,∠BAM=60°,
∵∠ABC=90°,
∴AM=AB,
∵△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∴AM=BD,∠ABD=∠BAM,
∵∠BND=∠ANM,
∴△AMN≌△BDN,
∴AN=NB.
 解:连接AM,
解:连接AM,∵M为CE边中点,△ACE是等边三角形,
∴AM⊥EC,
∠CAM=30°,
∵∠BAC=30°,
∴∠BAC=∠CAM,∠BAM=60°,
∵∠ABC=90°,
∴AM=AB,
∵△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∴AM=BD,∠ABD=∠BAM,
∵∠BND=∠ANM,
∴△AMN≌△BDN,
∴AN=NB.
点评:此题考查了等边三角形的性质,用到的知识点是等边三角形的性质,三角形的全等,角平分线的性质等,解题的关键是作出辅助线,证明△AMN≌△BDN.

练习册系列答案
相关题目
在平面直角坐标系中,点(9π,-5)位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,在Rt△ABC中,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,求△AEF面积最大为
如图,在Rt△ABC中,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,求△AEF面积最大为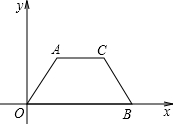 如图所示,梯形AOBC中,AC∥OB,AO=CB,A(2,2
如图所示,梯形AOBC中,AC∥OB,AO=CB,A(2,2

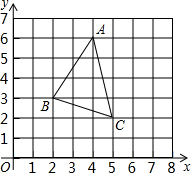 如图,△ABC的顶点坐标分别为A(4,6)、B(2,3)、C(5,2)
如图,△ABC的顶点坐标分别为A(4,6)、B(2,3)、C(5,2) 如图所示平行四边形ABCD中,E是BC上一点,且
如图所示平行四边形ABCD中,E是BC上一点,且