题目内容
 如图,在△ABC中,AB=3cm,AC=4cm,BC=5cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E.线段DE的最小值是
如图,在△ABC中,AB=3cm,AC=4cm,BC=5cm,M是BC边上的动点,MD⊥AB,ME⊥AC,垂足分别是D、E.线段DE的最小值是考点:矩形的判定与性质,垂线段最短,勾股定理的逆定理
专题:
分析:利用勾股定理逆定理判断出∠A=90°,再根据有三个角是直角的四边形是矩形判断出四边形ADME是矩形,根据矩形的对角线相等可得AM=DE,再根据垂线段最短可得AM⊥BC时,线段DE最小,然后利用△ABC的面积列出方程求解即可.
解答: 解:∵AB2+AC2=32+42=25=BC2,
解:∵AB2+AC2=32+42=25=BC2,
∴∠A=90°,
又∵MD⊥AB,ME⊥AC,
∴四边形ADME是矩形,
连接AM,则AM=DE,
由垂线段最短可知,AM⊥BC时,线段DE最小,
此时,S△ABC=
×5AM=
×3×4,
解得AM=2.4,
即DE=2.4cm.
故答案为:2.4.
 解:∵AB2+AC2=32+42=25=BC2,
解:∵AB2+AC2=32+42=25=BC2,∴∠A=90°,
又∵MD⊥AB,ME⊥AC,
∴四边形ADME是矩形,
连接AM,则AM=DE,
由垂线段最短可知,AM⊥BC时,线段DE最小,
此时,S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
解得AM=2.4,
即DE=2.4cm.
故答案为:2.4.
点评:本题考查了矩形的判定与性质,勾股定理逆定理,垂线段最短的性质,判断出四边形ADME是矩形并得到AM=DE是解题的关键,难点在于判断出AM⊥BC时,线段DE最小.

练习册系列答案
相关题目
 如图,线段AB=2cm,把线段AB向右平移3cm,得到线段DC,连接BC、AD,则四边形ABCD的面积为( )
如图,线段AB=2cm,把线段AB向右平移3cm,得到线段DC,连接BC、AD,则四边形ABCD的面积为( )| A、4cm2 |
| B、9cm2 |
| C、6cm2 |
| D、无法确定 |
 如图,已知:DF∥AC,∠C=∠D.
如图,已知:DF∥AC,∠C=∠D.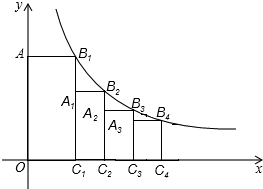 如图,点B1在反比例函数y=
如图,点B1在反比例函数y= 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1,A2,A3,A4,…表示,则顶点A55的坐标是 如图,在正方形ABCD中,对角线长为6,E是AB边上的任意一点,EM⊥AC,EN⊥BD,垂足分别是M、N,则EM+EN=
如图,在正方形ABCD中,对角线长为6,E是AB边上的任意一点,EM⊥AC,EN⊥BD,垂足分别是M、N,则EM+EN= 如图,?ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为
如图,?ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为