题目内容

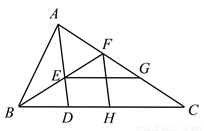
如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,H为BC上一点，且BH=BA交AC于点F,连接FH.

⑴求证:AE=FH;

⑵作EG//BC交AC于点G若AG=5，AC=8，求FG的长.

（1）详见解析；（2）FG=2 【解析】试题分析：（1）由角平分线的定义和已知条件证出∠AFB=∠AEF，即可得AE=AF，再利用SAS证明△ABF≌△HBF，得出AF=FH，即可得结论；（2）证明△AEG≌△FHC，得出AG=FC=5，即可得出结果． 试题解析： （1）∵BF平分∠ABC， ∴∠ABF=∠CBF； ∵∠AFB=180°-∠ABF－∠BAF，∠BED=...
练习册系列答案
相关题目

若关于的分式方程 无解,则的值为________.

2或1 【解析】 去分母得， 2(x-2)+(1-kx)=-1, 整理得 (2-k)x=2， ∴当2-k=0时或x-2=0时原方程无解. 当2-k=0时，k=2; 当x-2=0时，即x=2时，2-k=1,k=1. ∴当，k=2或k=1时，原方程无解.

在-6，0，3，8这四个数中，最小的数是( )

A. -6 B. 0 C. 3 D. 8

A 【解析】试题分析：数的大小比较法则为：正数大于一切负数；零大于负数，零小于正数；两个正数比较大小，绝对值大的数大；两个负数比较大小，绝对值大的数反而小．本题中最小的数为-6，选A．

将抛物线y=﹣3x2平移，得到抛物线y=﹣3 （x﹣1）2﹣2，下列平移方式中，正确的是（　　）

A. 先向左平移1个单位，再向上平移2个单位

B. 先向左平移1个单位，再向下平移2个单位

C. 先向右平移1个单位，再向上平移2个单位

D. 先向右平移1个单位，再向下平移2个单位

D 【解析】将抛物线y=-3x2平移，先向右平移1个单位得到抛物线y=-3（x-1）2, 再向下平移2个单位得到抛物线y=-3（x-1）2-2. 故选D.

抛物线y=（x﹣1）2+3的顶点坐标是（　　）

A. （1，3） B. （﹣1，3） C. （﹣1，﹣3） D. （1，﹣3）

A 【解析】∵y=(x?1)²+3， ∴顶点坐标为(1,3)， 故选A.

如图，将六边形纸片ABCDEF沿虚线剪去一个角(∠BCD)后，得到∠1＋∠2＋∠3＋∠4＋∠5＝400°，求∠BGD的度数．

40° 【解析】试题分析：根据多边形的内角和公式，求得六边形ABCDEF的内角和，又由∠1+∠2+∠3+∠4+∠5=400°，即可求得∠GBC+∠C+∠CDG的度数，再根据四边形的内角和为360度，即可求得∠BGD的度数． 试题解析： ∵六边形ABCDEF的内角和为：180°×（6-2）=720°，且∠1+∠2+∠3+∠4+∠5=400°， ∴∠GBC+∠C+∠CDG=72...

如图△ABC与△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )

A. 115° B. 120° C. 125° D. 130°

C 【解析】因为△ABC和△CDE都是等边三角形， ∴AC=BC,CE=CD,∠BAC=60°,∠ACB=∠ECD=60°， ∴∠ACB?∠ECB=∠ECD?∠ECB， ∴∠ACE=∠BCD， 在△ACE和△BCD中， ∴△ACE≌△BCD(SAS)， ∴∠CAE=∠CBD， ∵∠EBD=65°， ∴65??∠EBC=60°?∠BAE， ...

一个角的余角比它的补角的大15°，求这个角的度数．

这个角是40°． 【解析】 试题分析：设这个角为x°，则它的余角为（90°-x），补角为（180°-x），再根据题中给出的等量关系列方程即可求解． 试题解析：设这个角的度数为x，则它的余角为（90°-x），补角为（180°-x）， 依题意，得：（90°-x）-（180°-x）=15°， 解得x=40°． 答：这个角是40°．

一元二次方程x2﹣2=0的根为（　　）

A. x=2 B. C. x=±2 D. ，

D 【解析】x2﹣2=0， 移项得：x2=2， 两边开平方得：x=±， ∴x1=，x2=﹣ ， 故选D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网