题目内容
用因式分解法解方程：9（2x+3）2=4（2x-5）2．
考点：解一元二次方程-因式分解法
专题：
分析：移项后用平方差公式解答．
解答：解：移项得，9（2x+3）2-4（2x-5）2=0，
因式分解得，[3（2x+3）-2（2x-5）][3（2x+3）+2（2x-5）]=0，
（6x+9-4x+10）（6x+9+4x-10）=0，
（2x+19）（10x-1）=0，
解得x1=-
，x2=
．
因式分解得，[3（2x+3）-2（2x-5）][3（2x+3）+2（2x-5）]=0，
（6x+9-4x+10）（6x+9+4x-10）=0，
（2x+19）（10x-1）=0，
解得x1=-
| 19 |
| 2 |
| 1 |
| 10 |
点评：本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
嫦娥三号月球探测器于2013年12月2日从西昌卫星发射中心顺利升空，当嫦娥三号卫星到达距月球200千米位置时，需要进行减速制动．只有这样，才能被月球引力捕获，成为绕月飞行的卫星．如果将200千米精确到米并用科学记数法表示，结果是（ ）
| A、2×102 |
| B、2×104 |
| C、2×105 |
| D、2×108 |
已知a2-4a+1=0，则a2+
=（ ）
| 1 |
| a2 |
| A、12 | B、13 | C、14 | D、15 |
若x2m-1y与x5ym+n是同类项，那么（mn+5）2008=（ ）
| A、1 | B、-1 |
| C、1或-1 | D、无法确定 |
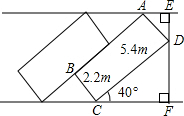随着人民生活水平的提高，小轿车也逐渐进入千家万户．为了解决停车难问题，我县交警大队在城区划定了许多机动车停车位．如图，矩形ABCD的供一辆机动车停放的车尾示意图，已知BC=2.2m，∠DCF=40°，请计算车位所占街道的宽度EF．（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，结果精确到0.1m）
有一块三角形木板，已测得边AB=50cm，∠B=35°，∠C=75°，求该板的面积．（精确到0.1cm2）