题目内容
已知a2-4a+1=0，则a2+
=（ ）
| 1 |
| a2 |
| A、12 | B、13 | C、14 | D、15 |
考点：分式的混合运算
专题：计算题
分析：法1：由已知求出a的值，代入计算即可确定出a2+
的值；
法2：已知等式两边除以a变形得到关系式，两边平方即可求出所求式子的值．
| 1 |
| a2 |
法2：已知等式两边除以a变形得到关系式，两边平方即可求出所求式子的值．
解答：解：法1：∵a2-4a+1=0，
∴（a-2）2-3=0，
∴a=2±
，
当a=2+
时，a2+
=（a+
）2-2=（2+
+
）2-2=14；
当a=2-
时，a2+
=（a+
）2-2=（2-
+
）2-2=14．
综上a2+
=14；
法2：已知方程变形得：a+
=4，
两边平方得：（a+
）2=a2+
+2=16，
则a2+
=14．
故选：C．
∴（a-2）2-3=0，
∴a=2±
| 3 |
当a=2+
| 3 |
| 1 |
| a2 |
| 1 |
| a |
| 3 |
| 1 | ||
2+
|
当a=2-
| 3 |
| 1 |
| a2 |
| 1 |
| a |
| 3 |
| 1 | ||
2-
|
综上a2+
| 1 |
| a2 |
法2：已知方程变形得：a+
| 1 |
| a |
两边平方得：（a+
| 1 |
| a |
| 1 |
| a2 |
则a2+
| 1 |
| a2 |
故选：C．
点评：此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
在下面的汽车标志图形中，是中心对称图形但不是轴对称图形有（ ）
A、 |
B、 |
C、 |
D、 |
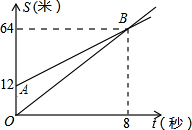如图，OB、AB分别表示甲、乙两名同学运动的一次函数图象，图中s和t分别表示运动路程和时间．已知甲的速度比乙快，下列说法：①射线AB表示甲的路程与时间的函数关系；②甲的速度比乙快10.5m/s；③甲让乙先跑了12m；④8秒钟后，甲超过了乙，其中正确的说法是（ ）| A、①② | B、②③④ |
| C、②③ | D、①③④图3 |
在代数式：①2x2，②-3，③x-2y，④t中，单项式个数是（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
点P（m+1，n）向下平移4个单位后，关于y轴对称的点的坐标为（-1，-5），则点P的坐标为（ ）
| A、（1，-1） |
| B、（1，1） |
| C、（-1，1） |
| D、（-1，-1） |
如图，白云养鸡场要建一个面积为150m2的长方形鸡场，为了节约材料，鸡场的一边靠墙，墙长am，另三边用竹篱笆围成，篱笆长为35m，篱笆墙的长和宽各是多少？