题目内容
已知x2-3x+1=0,求分式
的值.
| x7+7x4+x |
| x8+3x4+1 |
考点:分式的化简求值
专题:计算题
分析:已知等式变形求出x+
的值,两边平方,利用完全平方公式变形求出x2+
的值,同理求出x4+
的值,利用多项式乘以多项式法则求出x3+
的值,分别求出所求式子的分子分母,即可得到结果.
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x4 |
| 1 |
| x3 |
解答:解:由x2-3x+1=0,得x2+1=3x,
明显x≠0,等式两边可以同时除以x,得x+
=3①,
两边平方,得x2+2+
=9,即 x2+
=7②,
②两边再平方,得x4+2+
=49,即x4+
=47③,
①×②,得x3+
+x+
=21,即x3+3+
=21,
∴x3+
=18④,
根据①②③④,得:x7+7x4+x=x4•
=x4•(x3+7+
)=x4(18+7)=25x4,
同样的,分母部分为x8+3x4+1=x4•
=x4(x4+3+
)=x4(47+3)=50x4,
则原式=
.
明显x≠0,等式两边可以同时除以x,得x+
| 1 |
| x |
两边平方,得x2+2+
| 1 |
| x2 |
| 1 |
| x2 |
②两边再平方,得x4+2+
| 1 |
| x4 |
| 1 |
| x4 |
①×②,得x3+
| 1 |
| x |
| 1 |
| x3 |
| 1 |
| x3 |
∴x3+
| 1 |
| x3 |
根据①②③④,得:x7+7x4+x=x4•
| x7+7x4+x |
| x4 |
| 1 |
| x3 |
同样的,分母部分为x8+3x4+1=x4•
| x8+3x4+1 |
| x4 |
| 1 |
| x4 |
则原式=
| 1 |
| 2 |
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
下列运算正确的是( )
| A、-24=16 | ||
| B、-(-2)=2 | ||
C、(-
| ||
| D、(-2)3=8 |
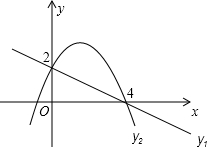 如图,已知直线y1=kx+b1与抛物线y2=-x2+b2x+c都经过点(4,0)和(0,2)
如图,已知直线y1=kx+b1与抛物线y2=-x2+b2x+c都经过点(4,0)和(0,2)