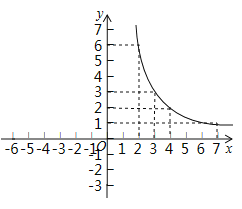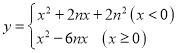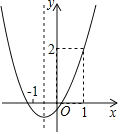题目内容
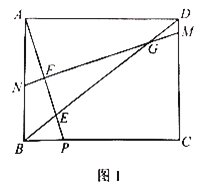
【题目】如图,某办公大楼正前方有一根高度是15米的旗杆![]() ,从办公大楼顶端
,从办公大楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是45°,旗杆底端
是45°,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是10米,梯坎坡长
是10米,梯坎坡长![]() 是10米,梯坎坡度
是10米,梯坎坡度![]() =1:
=1:![]() ,则大楼
,则大楼![]() 的高为______米.
的高为______米.
【答案】27
【解析】
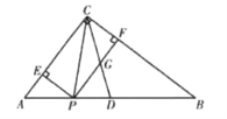
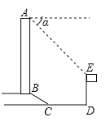
延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=HG,设BH=x米,则CH=![]() x米,在Rt△BCH中,BC=10米,由勾股定理得出方程,解方程求出BH=6米,CH=8米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=10+8=18(米),即可得出大楼AB的高度.
x米,在Rt△BCH中,BC=10米,由勾股定理得出方程,解方程求出BH=6米,CH=8米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=10+8=18(米),即可得出大楼AB的高度.
延长AB交DC于H,作EG⊥AB于G,如图所示:

则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:![]() ,
,
∴BH:CH=1:![]() ,
,
设BH=x米,则CH=![]() x米,
x米,
在Rt△BCH中,BC=10米,
由勾股定理得:x2+(![]() x)2=102,
x)2=102,
解得:x=6(负值舍去),
∴BH=6米,CH=8米,
∴BG=GH-BH=15-6=9(米),EG=DH=CH+CD=8+10=18(米),
∵∠α=45°,
∴∠EAG=90°-45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=18(米),
∴AB=AG+BG=9+18=27(米).
故答案为:27.

 阅读快车系列答案
阅读快车系列答案【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是________________;
的取值范围是________________;
(2)用描点法画函数图象:
①列表:
| … | -5 | -2 | -1 | 0 | … | 2 | 3 | 4 | 7 | … |
| … |
| 2 | 3 |
| … | 6 | 3 | 2 | 1 | … |
表中![]() 的值为______________,
的值为______________,![]() 的值为_______________.
的值为_______________.
②描点连线:请在右图画出该图象的另一部分.
(3)观察函数图象,得到函数![]() 的性质之一:当
的性质之一:当![]() _____________时,函数值
_____________时,函数值![]() 随
随![]() 的增大而增大.
的增大而增大.
(4)应用:若![]() ,则
,则![]() 的取值范围是______________.
的取值范围是______________.