题目内容
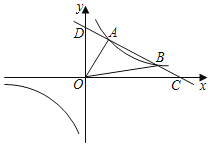
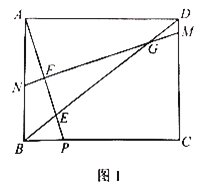
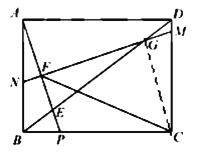
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
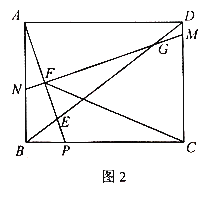
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由等角对等边可得![]() ,再由对顶角相等推出
,再由对顶角相等推出![]() ,然后利用等角的余角相等即可得证;
,然后利用等角的余角相等即可得证;
(2)在![]() 中,利用勾股定理可求出BD=10,然后由等角对等边得到
中,利用勾股定理可求出BD=10,然后由等角对等边得到![]() ,进而求出BP=2,再利用
,进而求出BP=2,再利用![]() 推出
推出![]() ,由垂直平分线推出
,由垂直平分线推出![]() ,即可得到
,即可得到![]() 的值;
的值;
(3)连接CG,先由勾股定理求出![]() ,由(2)的条件可推出BE=DG,再证明△ABE≌△CDG,从而求出
,由(2)的条件可推出BE=DG,再证明△ABE≌△CDG,从而求出![]() ,并推出
,并推出![]() ,最后在
,最后在![]() 中,即可求出
中,即可求出![]() 的值.
的值.
(1)证明:![]() ,
,
![]()
![]()
![]()
∵MN⊥AP
∴∠GFE=90°
∴∠BGN+∠GEF=90°
又![]()
![]()
![]()
(2)在矩形ABCD中,![]()
∴在![]() 中,
中,![]()
![]()
又∵在矩形ABCD中,![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴![]()
![]()
![]()
∵MN垂直平分AP
![]()
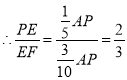
(3)如图,连接CG,
在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
又∵在矩形ABCD中,![]()
![]()
在△ABE和△CDG中,
∵AB=DC,∠ABE=∠CDG,BE=DG
![]()
![]()
![]()
![]()
![]()
∴在![]() 中,
中,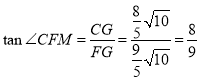

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为5元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格为6元/
的价格为6元/![]() ,超过
,超过![]() 部分的价格为4元/
部分的价格为4元/![]() .设小张在同一个批发店一次购买苹果的数量为
.设小张在同一个批发店一次购买苹果的数量为![]() .
.
(1)根据题意填表:
一次购买数量/ | 20 | 50 | 150 | … |
甲批发店花费/元 | 250 | … | ||
乙批发店花费/元 | 350 | … |
(2)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若小张在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小张在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的___________批发店购买花费少;
,则他在甲、乙两个批发店中的___________批发店购买花费少;
③若小张在同一个批发店一次购买苹果花费了460元,则他在甲、乙两个批发店中的___________批发店购买数量多.