题目内容
19. 如图,有一张长为7宽为5的矩形纸片ABCD,要通过适当的剪拼,得到一个与之面积相等的正方形.
如图,有一张长为7宽为5的矩形纸片ABCD,要通过适当的剪拼,得到一个与之面积相等的正方形.(Ⅰ)该正方形的边长为$\sqrt{35}$(结果保留根号);
(Ⅱ)现要求只能用两条裁剪线,请你设计一种裁剪的方法.在图中画出裁剪线,并简要说明裁剪的过程.
分析 (I)设正方形的边长为a,则a2=7×5,可解得正方形的边长;
(II)以BM=6为直径作半圆,在半圆上取一点N,使MN=1,连接BN,则∠MNB=90°,由勾股定理,得BN=$\sqrt{{6}^{2}-{1}^{2}}$=$\sqrt{35}$,由此构造正方形的边长,利用平移法画正方形.
解答 解:(I)设正方形的边长为a,则a2=7×5,
解得a=$\sqrt{35}$;
(II)如图,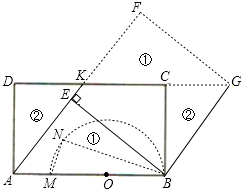
(1)以BM=6为直径作半圆,在半圆上取一点N,使MN=1,连接BN,由勾股定理,得BN=$\sqrt{B{M}^{2}-M{N}^{2}}$=$\sqrt{35}$;
(2)以A为圆心,BN长为半径画弧,交CD于K点,连接AK,
(3)过B点作BE⊥AK,垂足为E,
(4)平移△ABE,△ADK,得到四边形BEFG即为所求.
故答案为:$\sqrt{35}$.
点评 此题考查了图形的剪拼,用到的知识点是勾股定理、矩形的性质、正方形的性质等,关键是利用有关性质通过空间想象画出图形.

练习册系列答案
相关题目
10.下列各式一定成立的是( )
| A. | (2x-y)2=4x2-2xy+y2 | B. | (a-b)2=(b-a)2 | ||
| C. | ($\frac{1}{2}$a-b)2=$\frac{1}{4}$a2+ab+b2 | D. | (x+2y)2=x2+4y2 |
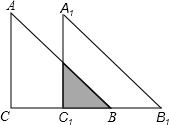 如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,
如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置, 如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F. 某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数,其图象如下图所示.
某校科技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强P(Pa)是木板面积S(m2)的反比例函数,其图象如下图所示. 如图,已知船C在观测站A的北偏东35°方向上,且在观测站B的北偏西20°方向上,那么∠ACB=55度.
如图,已知船C在观测站A的北偏东35°方向上,且在观测站B的北偏西20°方向上,那么∠ACB=55度.