题目内容
已知△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,添加下面的哪一个条件一定能使这两个三角形全等?
( )
( )
| A、∠C=∠C′ |
| B、AB=B′C′ |
| C、AC=A′C′ |
| D、AB=AC |
考点:全等三角形的判定
专题:
分析:根据三角形全等的判定条件可得应添加一对对应边相等,进而可得答案.
解答:解:因为存在条件∠A=∠A′,∠B=∠B′,
所以应该再添加一对对应边相等,故应添加AC=A′C′,
故选:C.
所以应该再添加一对对应边相等,故应添加AC=A′C′,
故选:C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若抛物线y=(1+m)xm2-2的开口向下,则m的值为( )
| A、2 | B、-2 | C、±2 | D、1 |
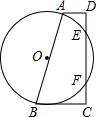 如图,在直角梯形ABCD中,∠C为直角,以AB为直径画圆,与CD相交于点E,F,已知AB=20,EF=16,那么AD+BC=
如图,在直角梯形ABCD中,∠C为直角,以AB为直径画圆,与CD相交于点E,F,已知AB=20,EF=16,那么AD+BC= 如图,△ABC中,∠BAC=68°,∠ACB=72°,∠ACB的平分线与∠BAC的外角平分线交于点D,连接BD,则∠BDC的大小等于
如图,△ABC中,∠BAC=68°,∠ACB=72°,∠ACB的平分线与∠BAC的外角平分线交于点D,连接BD,则∠BDC的大小等于 如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,则∠ACD的度数为
如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,则∠ACD的度数为