题目内容
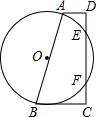 如图,在直角梯形ABCD中,∠C为直角,以AB为直径画圆,与CD相交于点E,F,已知AB=20,EF=16,那么AD+BC=
如图,在直角梯形ABCD中,∠C为直角,以AB为直径画圆,与CD相交于点E,F,已知AB=20,EF=16,那么AD+BC=考点:垂径定理,勾股定理,梯形中位线定理
专题:
分析:先根据AB=20求出OA的长,再过点O作OH⊥EF于点H,连接OF,根据垂径定理求出HF的长,由勾股定理求出OH的长,根据梯形中位线定理即可得出结论.
解答: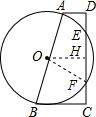 解:∵AB是⊙O的直径,AB=20,
解:∵AB是⊙O的直径,AB=20,
∴OA=
AB=10.
点O作OH⊥EF于点H,连接OF,
∵EF=16,
∴HF=
EF=8,
∴OH=
=
=6.
∵梯形ABCD是直角梯形,∠C为直角,
∴AD∥BC.
∵点O是直径AB的中点,
∴OH是梯形ABCD的中位线,
∴AD+BC=2OH=12.
故答案为:12.
 解:∵AB是⊙O的直径,AB=20,
解:∵AB是⊙O的直径,AB=20,∴OA=
| 1 |
| 2 |
点O作OH⊥EF于点H,连接OF,
∵EF=16,
∴HF=
| 1 |
| 2 |
∴OH=
| OF2-HF2 |
| 102-82 |
∵梯形ABCD是直角梯形,∠C为直角,
∴AD∥BC.
∵点O是直径AB的中点,
∴OH是梯形ABCD的中位线,
∴AD+BC=2OH=12.
故答案为:12.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有理数a,b在数轴上的位置如图所示,下列判断正确的是( )
有理数a,b在数轴上的位置如图所示,下列判断正确的是( )| A、a>0 | B、a>b |
| C、a+b>0 | D、ab>0 |
已知△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,添加下面的哪一个条件一定能使这两个三角形全等?
( )
( )
| A、∠C=∠C′ |
| B、AB=B′C′ |
| C、AC=A′C′ |
| D、AB=AC |
 如图是一次函数y=(k-2)x+b的图象,则k的取值范围是
如图是一次函数y=(k-2)x+b的图象,则k的取值范围是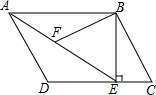 如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.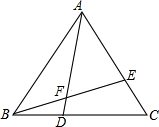 如图,在等边△ABC中,点D、E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.
如图,在等边△ABC中,点D、E分别是边BC、AC上的点,且BD=CE,连接BE、AD,相交于点F.