Question

11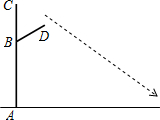．如图，望湖公园装有新型路灯，路灯设备由灯柱AC与支架BD共同组成（点C处装有安全监控，点D处装有照明灯），AC与地面垂直，BC为1.5米，BD为2米，AB为7米，∠CBD=60°，某一时刻，太阳光与地面的夹角为37°，求此时路灯设备整体在地面上的影长为多少？
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

Answer 1

分析 过点D作光线的平行线，交地面于点G，交射线AC于点F，过点D作DE⊥AF于点E，在Rt△DBE中，根据BE=BD•sin30°和DE=BD•cos30°求出BE和DE，在Rt△FED中，根据∠AGF=45°，求出EF=ED，再根据AF=AB+BE+EF，求出AF，然后与AC进行比较，即可得出路灯设备在地面上的影长．

解答 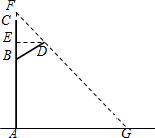解：如图，过点D作光线的平行线，交地面于点G，交射线AC于点F，过点D作DE⊥AF于点E，
在Rt△DBE中，
∵∠CBD=60°，
∴∠BDE=30°，
∵BD=2，
∴BE=BD•sin30°=1，DE=BD•cos30°=$\sqrt{3}$，
在Rt△FED中，
∵∠AGF=37°，
∴∠EDF=37°，
∴EF=ED•tan37°=$\frac{3\sqrt{3}}{4}$，
∵AB=7，
∴AF=AB+BE+EF=7+1+$\frac{3\sqrt{3}}{4}$=8+$\frac{3\sqrt{3}}{4}$．
∵8+$\frac{3\sqrt{3}}{4}$＞7，
∴此时的影长为AG．
在Rt△AFG中，AG=$\frac{AF}{tan37°}$=$\frac{32}{3}$+$\sqrt{3}$．
答：此刻路灯设备在地面上的影长为（$\frac{32}{3}$+$\sqrt{3}$）米．

点评 此题考查了解直角三角形，用到的知识点是锐角三角函数、三角形内角和定理，关键是根据题意画出图形，构造直角三角形．