题目内容
2.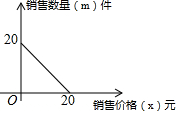 某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图象如图所示.
某商场以每件10元的价格购进一种商品,试销中发现,这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数,其函数图象如图所示.(1)求商场每天销售这种商品的销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)试判断,每件商品的销售价格在什么范围内,每天的销售利润随着价格的提高而增加.
分析 (1)直接利用待定系数法求出一次函数解析式进而得出销售利润y(元)与每件的销售价x(元)之间的函数解析式;
(2)直接得出二次函数对称轴进而利用二次函数增减性得出答案.
解答 解:(1)由图象,设一次函数解析式为:m=kx+b,
将(0,20),(20,0)代入得:$\left\{\begin{array}{l}{20k+b=0}\\{b=20}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=20}\end{array}\right.$,
故一次函数的解析式为:m=-x+20,
每件商品的利润为x-10,所以每天的利润为:
y=(x-10)(-x+20),
故函数解析式为:y=-x2+30x-200;
(2)∵x=-$\frac{30}{2×(-1)}$=15(元),
∴在0<x<15元时,每天的销售利润随着x的增大而增大.
点评 此题主要考查了二次函数的应用以及二次函数的增减性,正确得出二次函数解析式是解题关键.

练习册系列答案
相关题目
14. 学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
根据以上信息,解答下列问题.
(1)补全条形统计图.
(2)被统计学生投中篮的次数的中位数为2.平均数为1.8.
(3)若九年级有学生200人,请估计投中篮的次数在2次以上(包括2次)的人数.
 学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表.
学校开展阳光体育活动,组织九年级学生定点投篮,规定每人投篮3次.现对九年级(5)班每名学生投中篮的次数进行统计,并将统计结果绘制成如下不完整的统计图表. | 投中篮的次数(次) | 频数 (人数) | 频率 |
| 0 | 2 | 0.05 |
| 1 | 12 | 0.3 |
| 2 | x | 0.45 |
| 3 | 8 | y |
| 合计 | m | 1 |
(1)补全条形统计图.
(2)被统计学生投中篮的次数的中位数为2.平均数为1.8.
(3)若九年级有学生200人,请估计投中篮的次数在2次以上(包括2次)的人数.