Question

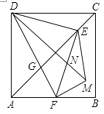
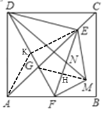
【题目】如图，正方形 ABCD 中，AD＝6，点 E 是对角线 AC 上一点，连接 DE，过点 E 作 EF⊥ ED，交 AB 于点 F，连接 DF，交 AC 于点 G，将△EFG 沿 EF 翻折，得到△EFM，连接DM，交 EF 于点 N，若点 F 是 AB 边的中点，则 △EDM 的面积是_____．

Answer 1

【答案】

【解析】

取DF的中点K，连接AK，KE，GM，得出点D、A、F、E四点共圆，进而得出△DEF是等腰直角三角形，通过已知数据计算出DF，DE，EF的长度，再由相似得出GF，由折叠的性质得到△GFM是等腰直角三角形，进而计算出MH，EH的长度，由△DEN∽△MHN得到EH的长度，最后由即可计算．

解：取DF的中点K，连接AK，KE，GM，

∵四边形ABCD是正方形，DE⊥EF，

∴∠DAF=90°，∠DAC=45°，

∴AK=，EK=，

∴点D、A、F、E四点共圆，

∴∠DFE=∠DAC=45°（同弧所对的圆周角相等），

∴△DEF是等腰直角三角形，

又∵AD=6，点 F 是 AB 边的中点，

∴AF=3，DF=，

∴DE=EF=，

又∵AF∥DC

△AGF∽△CGD

∴，即，

∴，

又∵△EFM是由△EFG翻折得到，

∴GM⊥EF，∠EFG=∠EFM=45°，GF=MF

∴△GFM是等腰直角三角形，

∴GM=，

∴MH=FH=，

∴EH=EF-FH=

又∵DE⊥EF，MH⊥EF，

∴△DEN∽△MHN

∴，即

∴，

∴，

=，

故答案为：．