Question

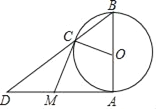
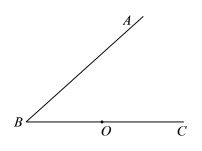
【题目】如图，点O为∠ABC的边上的一点，过点O作OM⊥AB于点，到点的距离等于线段OM的长的所有点组成图形．图形W与射线交于E，F两点(点在点F的左侧).

（1）过点作于点，如果BE=2，，求MH的长；

（2）将射线BC绕点B顺时针旋转得到射线BD，使得∠，判断射线BD与图形公共点的个数，并证明．

Answer 1

【答案】（1）MH=；（2）1个．

【解析】

（1）先根据题意补全图形，然后利用锐角三角函数求出圆的半径即OM的长度，再利用勾股定理求出BM的长度，最后利用可求出MH的长度.

（2）过点O作⊥于点，通过等量代换可知∠∠，从而利用角平分线的性质可知，得出为⊙的切线，从而可确定公共点的个数.

解：（1）∵到点的距离等于线段的长的所有点组成图形，

∴图形是以为圆心，的长为半径的圆．

根据题意补全图形：

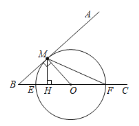
∵于点M，

∴∠．

在△中，

，

∴．

∵

∴，

解得：．

∴．

在△中，

，

∴．

∵

∴

∴．

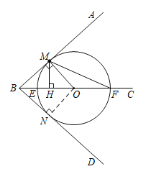
（2） 解： 1个．

证明：过点O作⊥于点，

∵∠∠，

且∠∠，

∴ ∠∠．

∴．

∴为⊙的切线．

∴射线与图形的公共点个数为1个．