题目内容
3. 如图,将一张长为70cm的矩形纸片ABCD沿对称轴EF折叠后得到如图所示的形状,若折叠后AB与CD的距离为60cm,则原纸片的宽度为( )
如图,将一张长为70cm的矩形纸片ABCD沿对称轴EF折叠后得到如图所示的形状,若折叠后AB与CD的距离为60cm,则原纸片的宽度为( )| A. | 20cm | B. | 15cm | C. | 10cm | D. | 30cm |
分析 设AB=xcm.根据轴对称图形的性质,得BE=DF=35-x(cm),从而再根据AB与CD间的距离为60cm,列方程求解.
解答 解:设AB=xcm.
根据轴对称图形的性质,得BE=DF=35-x(cm).
则有2(35-x)+x=60,
x=10.
∴AB=10cm,
即原纸片的宽度为10cm.
故选C.
点评 此题考查了折叠的性质与矩形的性质.此题难度适中,注意方程思想与数形结合思想的应用,设AB=xcm,能得到方程:2(35-x)+x=60是解此题的关键.

练习册系列答案
相关题目
18. 如图,△ABC是⊙O的内接三角形,∠A=25°,则∠OBC的度数为( )
如图,△ABC是⊙O的内接三角形,∠A=25°,则∠OBC的度数为( )
 如图,△ABC是⊙O的内接三角形,∠A=25°,则∠OBC的度数为( )
如图,△ABC是⊙O的内接三角形,∠A=25°,则∠OBC的度数为( )| A. | 50° | B. | 25° | C. | 65° | D. | 75° |
15.一种正方形瓷砖的面积是15平方分米,估计它的边长(单位:分米)在( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
12.将方程(x+1)(x-2)=2化为一元二次方程的一般形式,正确的是( )
| A. | x2-x-2=2 | B. | x2-x-4=0 | C. | x2-x=0 | D. | x2+x-4=0 |
13.下列各组数据分别是三角形三边长,是直角三角形的三边长的一组为( )
| A. | 5,6,7 | B. | 2,3,4 | C. | 8,15,17 | D. | 4,5,6 |
 如图,四边形ABCD中,对角线AC⊥BD,点E、F、G、H分别是AD、AB、BC、CD的中点.连接EF,FG,GH,EH,试探究:EFGH是怎样的特殊四边形?
如图,四边形ABCD中,对角线AC⊥BD,点E、F、G、H分别是AD、AB、BC、CD的中点.连接EF,FG,GH,EH,试探究:EFGH是怎样的特殊四边形? 如图,△ABC平移后得到△DEF,∠B=34°,∠A=66°,∠DEF=34°,∠F=80°.△ABC平移的距离是BE或CF的长度.
如图,△ABC平移后得到△DEF,∠B=34°,∠A=66°,∠DEF=34°,∠F=80°.△ABC平移的距离是BE或CF的长度.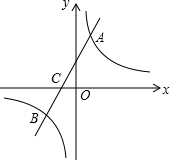 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2,点E在x轴上,若△ACE为直角三角形,则E的坐标是(1,0)、(13,0).
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2,点E在x轴上,若△ACE为直角三角形,则E的坐标是(1,0)、(13,0).