题目内容
11.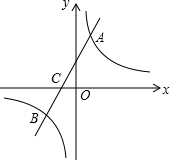 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2,点E在x轴上,若△ACE为直角三角形,则E的坐标是(1,0)、(13,0).
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2,点E在x轴上,若△ACE为直角三角形,则E的坐标是(1,0)、(13,0).
分析 利用待定系数法求得一次函数表达式,进而求得A( 1,6),进一步分两种情况分别讨论即可求得.
解答 解:∵C(-2,0),tan∠ACO=2,在一次函数y=kx+b,解得b=4,
∴一次函数表达式为 y=2x+4,
∵A( n,6)在直线y=2x+4上,解得n=1
∴A( 1,6)
∵∠ACE为锐角,
∴分两种情况讨论:
①∠AEC=90°时,E1 ( 1,0)
②∠EAC=90°时,△ACE1∽△AE1E2
∴AE12=CE1•E1E2
∴62=3E1E2
∴E1E2=12
∴E2 ( 13,0)
综上所述E1 ( 1,0)、E2 ( 13,0).
点评 此题考查了反比例函数与一次函数的交点问题.其知识点有待定系数法求解析式,三角形相似的判定和性质,解方程组等,此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 李明同学把自己一周的支出情况用如图所示的统计图来表示.则从图中可以看出( )
李明同学把自己一周的支出情况用如图所示的统计图来表示.则从图中可以看出( )
 李明同学把自己一周的支出情况用如图所示的统计图来表示.则从图中可以看出( )
李明同学把自己一周的支出情况用如图所示的统计图来表示.则从图中可以看出( )| A. | 一周支出的总金额 | |
| B. | 一周各项支出的金额 | |
| C. | 各项支出金额在一周中的变化情况 | |
| D. | 一周内各项支出金额占总支出的百分比 |
19.已知二次函数y=x2-4x+5的图象过点M(4,y1),N(-2,y2),K(-1,y3),则下列结论正确的是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y1<y3<y2 |
6.下列各数中,最大的数是( )
| A. | |-2| | B. | $\sqrt{2}$ | C. | -(-1.5) | D. | 20 |
16. 如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
(1)$\frac{BP}{AP}=\frac{AP}{AB}$;(2)AB:AP=AP:PB;(3)BP2=AP•AB;(4)$\frac{AP}{AB}$≈0.618.
 如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )
如图,P为线段AB的黄金分割点,且AP>BP,则下列结论成立的个数是( )(1)$\frac{BP}{AP}=\frac{AP}{AB}$;(2)AB:AP=AP:PB;(3)BP2=AP•AB;(4)$\frac{AP}{AB}$≈0.618.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3. 如图,将一张长为70cm的矩形纸片ABCD沿对称轴EF折叠后得到如图所示的形状,若折叠后AB与CD的距离为60cm,则原纸片的宽度为( )
如图,将一张长为70cm的矩形纸片ABCD沿对称轴EF折叠后得到如图所示的形状,若折叠后AB与CD的距离为60cm,则原纸片的宽度为( )
 如图,将一张长为70cm的矩形纸片ABCD沿对称轴EF折叠后得到如图所示的形状,若折叠后AB与CD的距离为60cm,则原纸片的宽度为( )
如图,将一张长为70cm的矩形纸片ABCD沿对称轴EF折叠后得到如图所示的形状,若折叠后AB与CD的距离为60cm,则原纸片的宽度为( )| A. | 20cm | B. | 15cm | C. | 10cm | D. | 30cm |