题目内容
如图，依次以三角形、四边形、…、n边形的各顶点为圆心画半径为1的圆，且圆与圆之间两两不相交．把三角形与各圆重叠部分面积之和记为S3，四边形与各圆重叠部分面积之和记为S4，…，n边形与各圆重叠部分面积之和记为Sn．则S12的值为 ．（结果保留π）
考点：多边形内角与外角
专题：规律型
分析：根据多边形的内角和公式求出n=12时的阴影部分的圆心角，再根据扇形面积公式列式计算即可得解．
解答：解：n=12时，多边形的内角和=（12-2）•180°=1800°，
所以，S12=
=5π．
故答案为：5π．
所以，S12=
| 1800•π•12 |
| 360 |
故答案为：5π．
点评：本题考查了多边形的内角和，扇形的面积计算，熟记公式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
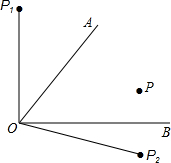如图，点P是∠AOB内部的一定点．
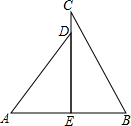两个直角三角形按如图方式摆放，若AD=10，BE=6，∠ADE=37°，∠BCE=29°．求CD长（精确到0.01）．
如图，菱形ABCD的边长是2cm，E是AB中点，且DE⊥AB，则DE的长为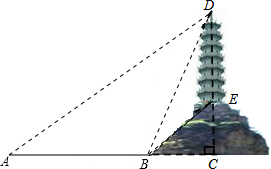
兴趣小组在一次数学实践活动中，为了测量如图所示的小山顶的塔高，进行了如下的操作，首先在A处测得塔尖D的仰角为30°，然后沿AC方向前进72米到达山脚B处，此时测得塔尖D的仰角为60°，塔底E的仰角为45°，求塔高．（结果保留根号）下面四个命题，其中假命题是（ ）
| A、全等三角形是相似三角形 |
| B、所有的正方形都相似 |
| C、所有的等边三角形都相似 |
| D、所有的直角三角形都相似 |
请画出如图中空心圆柱的三视图．