题目内容
5.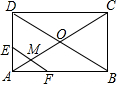 如图,在矩形ABCD中,对角线AC与BD相交于点O,点M为线段AC上一个动点,过点M作EF∥BD交AD(或DC)于点E,交AB(或BC)于点F,设AM=x,EF=y,则y关于x的函数图象大致形状是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,点M为线段AC上一个动点,过点M作EF∥BD交AD(或DC)于点E,交AB(或BC)于点F,设AM=x,EF=y,则y关于x的函数图象大致形状是( )| A. | 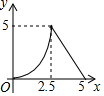 | B. | 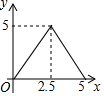 | C. | 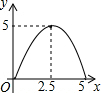 | D. | 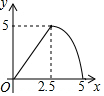 |
分析 当0≤x≤2.5时,如图1,根据矩形及平行线的性质得MA=ME=MF,知EF=2MA,即y=2x;当2.5<x≤5时,如图2,由题意知CM=AC-AM=5-x,由ME=MC=MF得EF=2MC,即y=2(5-x)=10-2x,即可得答案.
解答 解:当0≤x≤2.5时,如图1,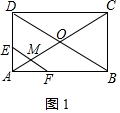
∵四边形ABCD是矩形,
∴OA=OB=OC=OD,
∴∠OAD=∠ODA,
∵EF∥BD,
∴∠ODA=∠MEA,
∴∠OAD=∠MEA,
∴MA=ME,同理可得MA=MF,
则EF=2MA,即y=2x;
当2.5<x≤5时,如图2,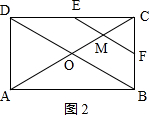
由题意知CM=AC-AM=5-x,
∵ME=MC=MF,
∴EF=2MC,即y=2(5-x)=10-2x;
综上,y=$\left\{\begin{array}{l}{2x}&{(0≤x≤2.5)}\\{10-2x}&{(2.5<x≤5)}\end{array}\right.$,
故选:B.
点评 本题主要考查动点问题的函数图象,熟练掌握矩形的性质和平行线的性质得出ME=MC=MF是解题的关键.

练习册系列答案
相关题目
16.不等式ax+b>0(a<0)的解集是( )
| A. | x>-$\frac{b}{a}$ | B. | x<-$\frac{b}{a}$ | C. | x>$\frac{b}{a}$ | D. | x<$\frac{b}{a}$ |
20.一组数据“3,3,4,5,5,5,6,6,7”的中位数是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 如图,将周长为4的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为4的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为( )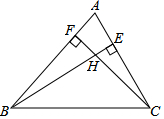 在△ABC中,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,
在△ABC中,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,