题目内容
10.小龙和晓丽用“红桃3”,“红桃4”,“梅花5”,“红桃6”这四张扑克牌玩游戏.(1)将这四张扑克牌洗牌后反扣在桌面上,翻开记下花色,再反扣洗牌,第二次翻开记下花色,若两次都是红桃,小龙赢;若是一次红桃一次梅花,则晓丽赢.小龙和晓丽谁赢的可能性大?说明理由;
(2)利用这四张扑克牌设计一个对于双方都公平的游戏方案,并说明理由.
分析 (1)根据题意可以写出所有的可能性,从而可以计算出小龙赢和晓丽赢的概率,从而可以解答本题;
(2)根据题意设计出符合要求的方案即可,然后通过计算方案中的概率说明理由即可解答本题.
解答 解:(1)小龙赢的可能性大,
理由:由题意可得,
出现的所有可能性是:
(红桃3,红桃3)、(红桃3,红桃4)、(红桃3,梅花5)、(红桃3,红桃6),
(红桃4,红桃3)、(红桃4,红桃4)、(红桃4,梅花5)、(红桃4,红桃6),
(梅花5,红桃3)、(梅花5,红桃4)、(梅花5,梅花5)、(梅花5,红桃6),
(红桃6,红桃3)、(红桃6,红桃4)、(红桃6,梅花5)、(红桃6,红桃6),
∴小龙赢的概率为:$\frac{9}{16}$,
晓丽赢的概率为:$\frac{6}{16}$,
∵$\frac{9}{16}>\frac{6}{16}$,
∴小龙赢得可能性大;
(2)对于双方都公平的游戏方案是:两次抽取的数的和为偶数是小龙赢,两次抽取的数的和为奇数时,晓丽赢.
理由:抽取的所有的两个数的和的可能性是:
3+3=6、3+4=7、3+5=8、3+6=9,
4+3=7、4+4=8、4+5=9、4+6=10,
5+3=8、5+4=9、5+5=10、5+6=11,
6+3=9、6+4=10、6+5=11、6+6=12,
∴两次抽取的数的和为偶数的概率是:$\frac{8}{16}=\frac{1}{2}$,
两次抽取的数的和为奇数的概率是:$\frac{8}{16}=\frac{1}{2}$,
∵$\frac{1}{2}=\frac{1}{2}$,
∴两次抽取的数的和为偶数是小龙赢,两次抽取的数的和为奇数时,晓丽赢,这种设计方案是合理的.
点评 本题考查游戏公平性、可能性大小,解答此类问题的关键是写出所有的可能性,求出相应的概率.

 阅读快车系列答案
阅读快车系列答案| 月份 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 人数 | 46 | 32 | 42 | 32 | 27 | 32 | 42 |
| A. | 46 | B. | 42 | C. | 32 | D. | 27 |
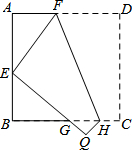 如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( )
如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( )| A. | 4:9 | B. | 2:3 | C. | 3:4 | D. | 9:16 |
| A. | 同角的余角相等 | |
| B. | 等腰三角形的两个底角相等 | |
| C. | 两直线平行,内错角相等 | |
| D. | 线段中垂线上的点到线段两端的距离相等 |
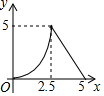
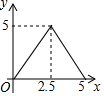
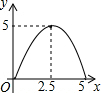
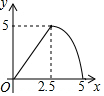
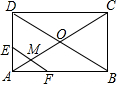 如图,在矩形ABCD中,对角线AC与BD相交于点O,点M为线段AC上一个动点,过点M作EF∥BD交AD(或DC)于点E,交AB(或BC)于点F,设AM=x,EF=y,则y关于x的函数图象大致形状是( )
如图,在矩形ABCD中,对角线AC与BD相交于点O,点M为线段AC上一个动点,过点M作EF∥BD交AD(或DC)于点E,交AB(或BC)于点F,设AM=x,EF=y,则y关于x的函数图象大致形状是( )