Question

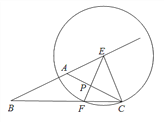
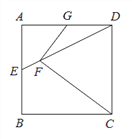
【题目】己知：如图，在正方形ABCD中，点E为边AB的中点，联结DE，点F在DE上CF=CD，过点F作FG⊥FC交AD于点G.

（1）求证：GF=GD；

（2）联结AF，求证：AF⊥DE.

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】分析：根据等角的余角相等得到即可证明.

联结CG.证明△DAE≌△CDG,得到.进而得到，根据等边对等角得到根据三角形的内角和可以求出∠AFD= 90°，即可证明.

详解：∵四边形是正方形，∴,

∵FG⊥FC， ∴∠GFC= 90°,

∵ ∴∠CDF=∠CFD ,

∴∠GFC-∠CFD=∠ADC-∠CDE，即∠GFD=∠GDF.

∴GF=GD.

联结CG.

∵ ∴点在线段的中垂线上,

∴GC⊥DE，

∴∠CDF+∠DCG= 90°，

∵∠CDF+∠ADE= 90°，

∴∠DCG=∠ADE.

四边形是正方形,

∴AD=DC，∠DAE=∠CDG= 90°，

∴△DAE≌△CDG,

∴.

点是边的中点，

点是边的中点，

∴,

∴

∵

∴

∴∠AFD= 90°，即AF⊥DE.