题目内容
1.正方形ABCD内一点P与点A、B组成等边三角形,则三角形PCD三个内角的度数分别为15°,15°,150°.分析 由正方形的性质得出∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,由等边三角形的性质得出∠ABP=∠BAP=60°,AB=PA=PB,求出∠PAD=30°,PA=AD,再由等腰三角形的性质和三角形内角和定理求出∠ADP=∠APD=75°,得出∠PDC=15°,同理:∠PCD=15°,再由三角形内角和定理求出∠CPD即可.
解答 解:如图所示: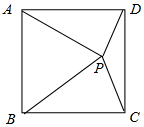
∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,
∵△PAB是等边三角形,
∴∠ABP=∠BAP=60°,AB=PA=PB,
∴∠PAD=90°-60°=30°,PA=AD,
∴∠ADP=∠APD=(180°-30°)÷2=75°,
∴∠PDC=90°-75°=15°,
同理:∠PCD=15°,
∴∠CPD=180°-2×15°=150°;
故答案为:15°,15°,150°.
点评 本题考查了正方形的性质、等边三角形的性质、等腰三角形的性质、三角形内角和定理;熟练掌握正方形和等边三角形的性质是解决问题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
11.下列各图中的角,其中为圆周角的是( )
| A. |  | B. |  | C. |  | D. |  |
12.若t是一元二次方程ax2+bx+c=0(a≠0)的根,则判别式b2-4ac和完全平方式M=(2at+b)2的关系是( )
| A. | b2-4ac=M | B. | b2-4ac>M | ||
| C. | b2-4ac<M | D. | 大小关系不能确定 |