题目内容
9.二次函数y=x2-2x-3,当m-2≤x≤m时的最大值为5,则m的值可能为( )| A. | 0或6 | B. | 4或-2 | C. | 0或4 | D. | 6或-2 |
分析 先求出抛物线的对称轴为直线x=-1,然后确定当x=4时取得最大值,代入函数解析式进行计算即可得解.
解答 解:y=x2-2x-3=(x-1)2-4,
∵抛物线的对称轴为直线x=1,
∴当-2≤x≤m<4时,x=-2时二次函数y=x2-2x-3的最大值为:y=4+4-3=5,符合题意;
当m≥4时,x=m时二次函数y=x2-2x-3的最大值为:m2-2m-3=5,
解得m1=4,m2=-2(舍去).
综上所述,m的值为0或4都符合题意,6和-2都不符合题意.
故选:C.
点评 本题考查了二次函数的最值问题,主要利用了二次函数的对称性,确定出抛物线的对称轴解析式是确定m的取值范围的关键,难点在于读懂题目信息.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.如图(1),PT与⊙O1相切于点T,PAB与⊙O1相交于A、B两点,可证明△PTA∽△PBT,从而有PT2=PA•PB,请应用以上结论解决下列问题:如图(2),PAB、PCD分别与⊙O2相交于A、B、C、D四点,已知PA=2,PB=7,PC=3,则CD=( )
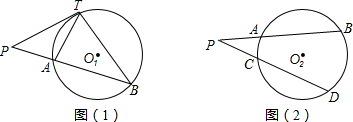

| A. | $\frac{14}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{5}{3}$ | D. | 4 |
17.某同学一次掷出两枚骰子,两枚骰子全是刻有数字“6”的面朝上的事件是( )
| A. | 不可能事件 | B. | 随机事件,可能性较大 | ||
| C. | 必然事件 | D. | 随机事件,可能性较小 |
4.计算(y-5)2的结果是( )
| A. | y2-25 | B. | y2-5y+25 | C. | y2+10y+25 | D. | y2-10y+25 |
14.下列运算正确的是( )
| A. | x•x5=x6 | B. | (-2a2)3=-6a6 | C. | (a+b)2=a2+b2 | D. | -2(a-1)=-2a+1 |
19.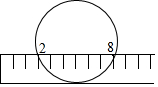 如图,当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处读数如图所示,那么该圆的半径长为( )
如图,当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处读数如图所示,那么该圆的半径长为( )
 如图,当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处读数如图所示,那么该圆的半径长为( )
如图,当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处读数如图所示,那么该圆的半径长为( )| A. | $\frac{25}{3}$ | B. | $\frac{25}{6}$ | C. | 5 | D. | 3 |
 如图,已知△ABC的面积为32,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为32,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( ) 在?ABCD中,AC的垂直平分线分别交AD,BC于F,E两点,交AC于O点,试判断四边形AECF的形状,并说明理由.
在?ABCD中,AC的垂直平分线分别交AD,BC于F,E两点,交AC于O点,试判断四边形AECF的形状,并说明理由.