题目内容
1. 如图,已知△ABC的面积为32,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )
如图,已知△ABC的面积为32,点D在线段AC上,点F在线段BC的延长线上,且BC=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )| A. | 8 | B. | 6 | C. | 4 | D. | 3 |
分析 连接EC,过A作AM∥BC交FE的延长线于M,求出平行四边形ACFM,根据等底等高的三角形面积相等得出△BDE的面积和△CDE的面积相等,△ADE的面积和△AME的面积相等,推出阴影部分的面积等于平行四边形ACFM的面积的一半,求出CF×hCF的值即可.
解答 解:连接EC,过A作AM∥BC交FE的延长线于M,
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE边DE上的高和△CDE的边DE上的高相同,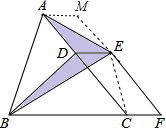
∴△BDE的面积和△CDE的面积相等,
同理△ADE的面积和△AME的面积相等,
即阴影部分的面积等于平行四边形ACFM的面积的一半,是$\frac{1}{2}$×CF×hCF,
∵△ABC的面积是32,BC=4CF
∴$\frac{1}{2}$BC×hBC=$\frac{1}{2}$×4CF×hCF=32,
∴CF×hCF=16,
∴阴影部分的面积是$\frac{1}{2}$×16=8,
故选A.
点评 本题考查了平行四边形的性质和判定,三角形的面积的应用,主要考查学生的推理能力和转化能力,题目比较好,但是有一定的难度.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
11.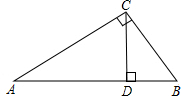 如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
 如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )| A. | 点A到BC的距离是AC的长度 | B. | 点B到AC的距离是BC的长度 | ||
| C. | 线段BD的长叫D到BC的距离 | D. | 在线段CA、CD、CB中,CD最短 |
9.二次函数y=x2-2x-3,当m-2≤x≤m时的最大值为5,则m的值可能为( )
| A. | 0或6 | B. | 4或-2 | C. | 0或4 | D. | 6或-2 |
16.直线y=kx-k一定经过点( )
| A. | (1,0) | B. | (1,k) | C. | (0,k) | D. | (0,-1) |
6.如图,某乡镇第一季度“家电下乡”产品的购买情况绘制成的两幅不完整的统计图,请根据统计图提供的信息解答下列问题:
(1)求第一季度购买的“家电下乡”产品的总台数;
(2)通过计算,把两幅统计图补充完整.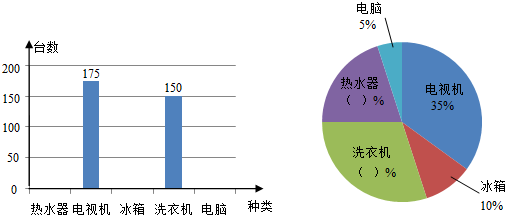
(1)求第一季度购买的“家电下乡”产品的总台数;
(2)通过计算,把两幅统计图补充完整.

13.在平面直角坐标系中,点P(a,a-1)在y轴上,那么点P的坐标是( )
| A. | (0,1) | B. | (-1,0) | C. | (1,0) | D. | (0,-1) |
10.用配方法解一元二次方程x2+3x-1=0,下列配方正确的是( )
| A. | ${({x+\frac{3}{2}})^2}=\frac{13}{4}$ | B. | ${({x+\frac{3}{2}})^2}=\frac{5}{4}$ | C. | (x+3)2=10 | D. | (x+3)2=8 |
11. 如图,这是我们常用的折叠式小刀,其中刀片的两条边缘线是两条平行的线段,右图为左图的局部放大图,则∠1+∠2为( )
如图,这是我们常用的折叠式小刀,其中刀片的两条边缘线是两条平行的线段,右图为左图的局部放大图,则∠1+∠2为( )
 如图,这是我们常用的折叠式小刀,其中刀片的两条边缘线是两条平行的线段,右图为左图的局部放大图,则∠1+∠2为( )
如图,这是我们常用的折叠式小刀,其中刀片的两条边缘线是两条平行的线段,右图为左图的局部放大图,则∠1+∠2为( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |