题目内容
12.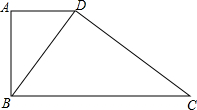 直角梯形ABCD中,AD∥BC,BA⊥AD,∠BDC=90°,其中AD=4米,BC=9米,则BD的长度为( )
直角梯形ABCD中,AD∥BC,BA⊥AD,∠BDC=90°,其中AD=4米,BC=9米,则BD的长度为( )| A. | 12米 | B. | 13米 | C. | 5米 | D. | 6米 |
分析 由梯形的性质得出∠ADB=∠DBC,证明△ABD∽△DCB,得出对应边成比例$\frac{AD}{BD}=\frac{BD}{BC}$,即可得出BD的长.
解答 解:∵BA⊥AD,
∴∠A=90°,
∴∠A=∠BDC=90°,
∵AD∥BC,
∴∠ADB=∠DBC,
∴△ABD∽△DCB,
∴$\frac{AD}{BD}=\frac{BD}{BC}$,
即BD2=AD×BC=4×9=36,
∴BD=6(米).
故选:D.
点评 本题考查了梯形的性质、相似三角形的判定与性质;熟练掌握梯形的性质,证明三角形相似得出对应边成比例是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若|a|=2,|b|=5,且a<b,则a+b=( )
| A. | 3 | B. | 7 | C. | 3或7 | D. | ±3或±7 |
1.对于如图①、②、③、④所示的四个平面图,我们规定:如图③,它的顶点为A、B、C、D、E共5个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条,区域为AED、ABE、BEC、CED共4个.

(1)按此规定,将图①、②、④的顶点数X、边数Y、区域数Z填入下面的表格:
(2)观察上表,请你归纳顶点数X、边数Y、区域数Z之间的数量关系.

(1)按此规定,将图①、②、④的顶点数X、边数Y、区域数Z填入下面的表格:
| 图 | 顶点数X | 边数Y | 区域数Z |
| ① | 4 | 6 | 3 |
| ② | 6 | 9 | 4 |
| ③ | 5 | 8 | 4 |
| ④ | 10 | 15 | 6 |
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a<0;②b>0;③b>2a;④a+b+c=2.其中正确的结论是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a<0;②b>0;③b>2a;④a+b+c=2.其中正确的结论是( ) 如图是由一个正方体和一个长方体组成的组合体
如图是由一个正方体和一个长方体组成的组合体 如图,这是一个可以自由转动的三色转盘,求出下列事件的概率:
如图,这是一个可以自由转动的三色转盘,求出下列事件的概率: