题目内容
20.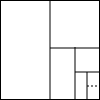 如图,有-个面积为1的正方形纸板,第一次剪掉这块正方形纸板的一半,第二次剪掉剩下的一半,以此类推.问:
如图,有-个面积为1的正方形纸板,第一次剪掉这块正方形纸板的一半,第二次剪掉剩下的一半,以此类推.问:(1)第3次剪掉的面积是$\frac{1}{8}$;第3次剪掉后剩下的面积是$\frac{1}{8}$;
(2)第n次剪掉的面积是$\frac{1}{{2}^{n}}$;第n次剪掉后剩下的面积是$\frac{1}{{2}^{n}}$;
(3)受此启发,请计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$…+$\frac{1}{{2}^{n}}$;
(4)第(3)小题我们是借助图形解决了数的运算问题,这是数形结合数学思想的应用.
分析 (1)(2)第1次剪掉的面积是$\frac{1}{2}$;第1次剪掉后剩下的面积是1-$\frac{1}{2}$=$\frac{1}{2}$;第2次剪掉的面积是$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$;第3次剪掉后剩下的面积是$\frac{1}{2}$×$\frac{1}{2}$=$\frac{1}{4}$;第3次剪掉的面积是$\frac{1}{8}$;第3次剪掉后剩下的面积是$\frac{1}{8}$;…由此规律得出答案即可;
(3)由此利用1减去最后剩下的面积计算得出$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$…+$\frac{1}{{2}^{n}}$的结果;
(4)数形结合的思想运用.
解答 解:(1)第3次剪掉的面积是$\frac{1}{8}$;第3次剪掉后剩下的面积是$\frac{1}{8}$;
(2)第n次剪掉的面积是$\frac{1}{{2}^{n}}$;第n次剪掉后剩下的面积是$\frac{1}{{2}^{n}}$;
(3)$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$;
(4)第(3)小题我们是借助图形解决了数的运算问题,这是数形结合数学思想的应用.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字运算规律,利用规律解决问题.

练习册系列答案
相关题目
 经过两个已知点A、B能确定一个圆吗?经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
经过两个已知点A、B能确定一个圆吗?经过两个已知点A、B所作的圆的圆心在怎样的一条直线上?
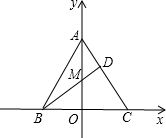 在平面直角坐标系中,已知A点在y轴正半轴上,B点在x轴负半轴上,C点在x轴正半轴上,BD是△ABC的高,且交y轴于点M.
在平面直角坐标系中,已知A点在y轴正半轴上,B点在x轴负半轴上,C点在x轴正半轴上,BD是△ABC的高,且交y轴于点M.