题目内容
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
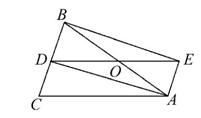
(1)求证:四边形AEBD是矩形.
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
【解析】(1)∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,∴∠ADB=90°,
∴平行四边形AEBD是矩形.即四边形AEBD是矩形.
(2)当∠BAC=90°时,矩形AEBD是正方形.理由:
∵∠BA C=90°,AB=AC,AD是△ABC的角平分线,
C=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1) 得四边形AEBD是矩形,
得四边形AEBD是矩形,
∴矩形AEBD是正方形.

练习册系列答案
相关题目
 12、11、9、 10、13.则这组数据的( )
12、11、9、 10、13.则这组数据的( ) ,则此三角形一定是( )
,则此三角形一定是( ) DC的平分线,F是AB的中点,AB=6,AD=4,则AE∶EF∶BE为( )
DC的平分线,F是AB的中点,AB=6,AD=4,则AE∶EF∶BE为( )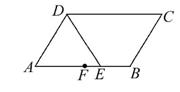

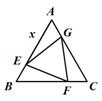

 ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为 .
 B.
B. C.
C. D.
D.
 ≌
≌ ,其理由是(简写) .
,其理由是(简写) . 